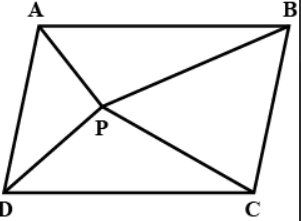
In Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
Given ABCD is a parallelogram. So, AB||CD,AD||BC.
(i) Now, draw MPR parallel to AB and CD both and also draw a perpendicular PS on AB.
.:MR||ABandAM||BR
∴ABRM is a parallelogram
∴Ar(∣∣gmABRM)=AB×PS...(1)
and ar(ΔAPB)=12×AB×PS
⇒ar(ΔAPB)=12ar(∣∣gmABRM) [from (1)]
Similarly, ar(ΔPCD)=12ar(∣∣gmMRCD)
Now, ar(ΔAPB)+ar(ΔPCD)=12ar(∣∣gmABRM)+12ar(∣∣gmMRCD)
=12ar(∣∣gmABCD)...(2)
(ii) Similarly, we can draw a line through P parallel to AD and through the point P draw perpendicular on AD, we can prove that
ar(ΔAPD)+ar(ΔPBC)=12ar(∣∣gmABCD)
From (2) and (3), we get
ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
In Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
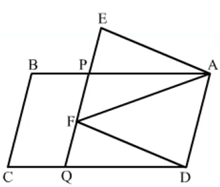
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
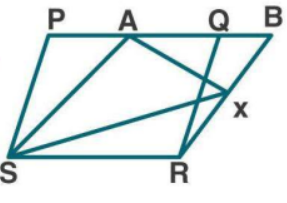
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
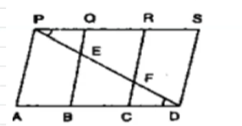
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View Solution
