In the figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ=QR=RS and PA||QB||RC. Prove that ar(PQE)=ar(CFD).
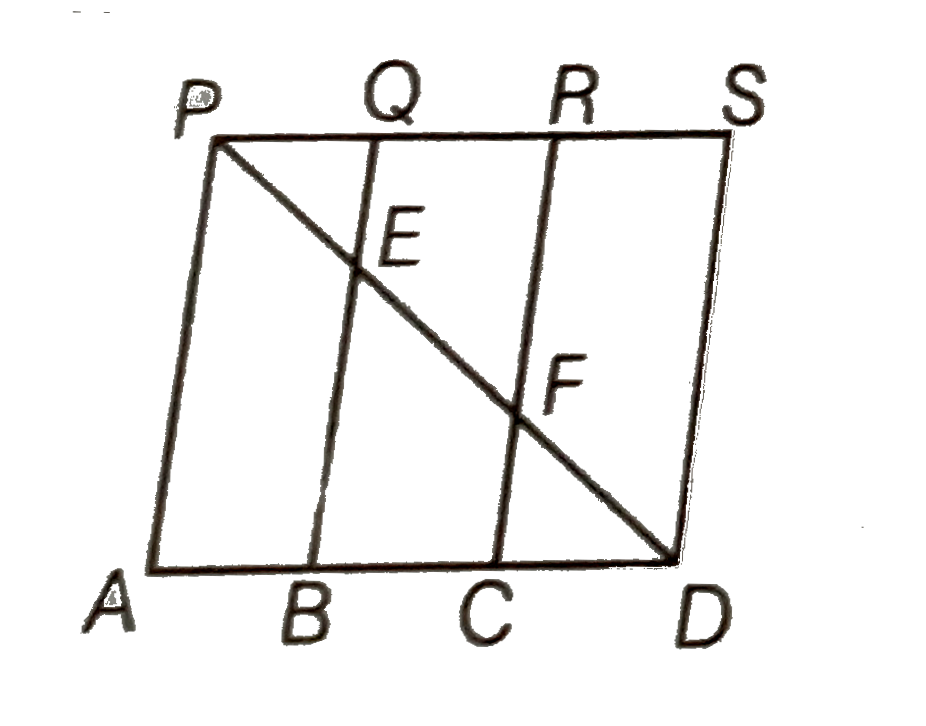
Given : PSDA is a parallelogram. Points Q and R are taken on PS such that PQ=QR=RSandPA||QB||RC.
To prove : ar(ΔPQE)=ar(ΔCFD)
Proof: Now, PS=AD (opposite side of a parallelogram)
∴13PS=13AD⇒PQ=CD...(1)
Again, PS∣∣AD and QB cut them.
∴∠PQE=∠CBE (alternate angles)...(2)
Now, QB∣∣RC and AD cuts them
∴∠QBD=∠RCD (corresponding angles)...(3)
So, ∠PQE=∠FCD...(4)
[from (2) and (3), ∠CBEand∠QBD are same and ∠RCDand∠FCD are same] ΔPQEandΔCFD
∵⎧⎪⎨⎪⎩∠QPE=∠CDF (alternate angles) PQ=CD [from(1)]∠PQE=∠FCD [from (4)]
∴ΔPQE≅ΔCFD (by ASA congruence rule)
Hence, ar(ΔPQE)=ar(ΔCFD) (congruent triangles are equal in area)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise34videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
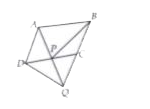
In the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
 View Solution
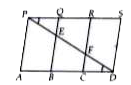
View SolutionIn the given figure PSDA is a parallelogram in which PQ =QR= RS and AP II BQ II CR II VS.Prove that ar(△PQE) = ar(△DCF).
 View Solution
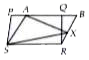
View SolutionIn the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar(PQRS) = ar(ABRS)
 View Solution
View SolutionIn the given figure, Q is a point on the side SR of ΔPSR such that PQ = PR. Prove that PS>PQ.
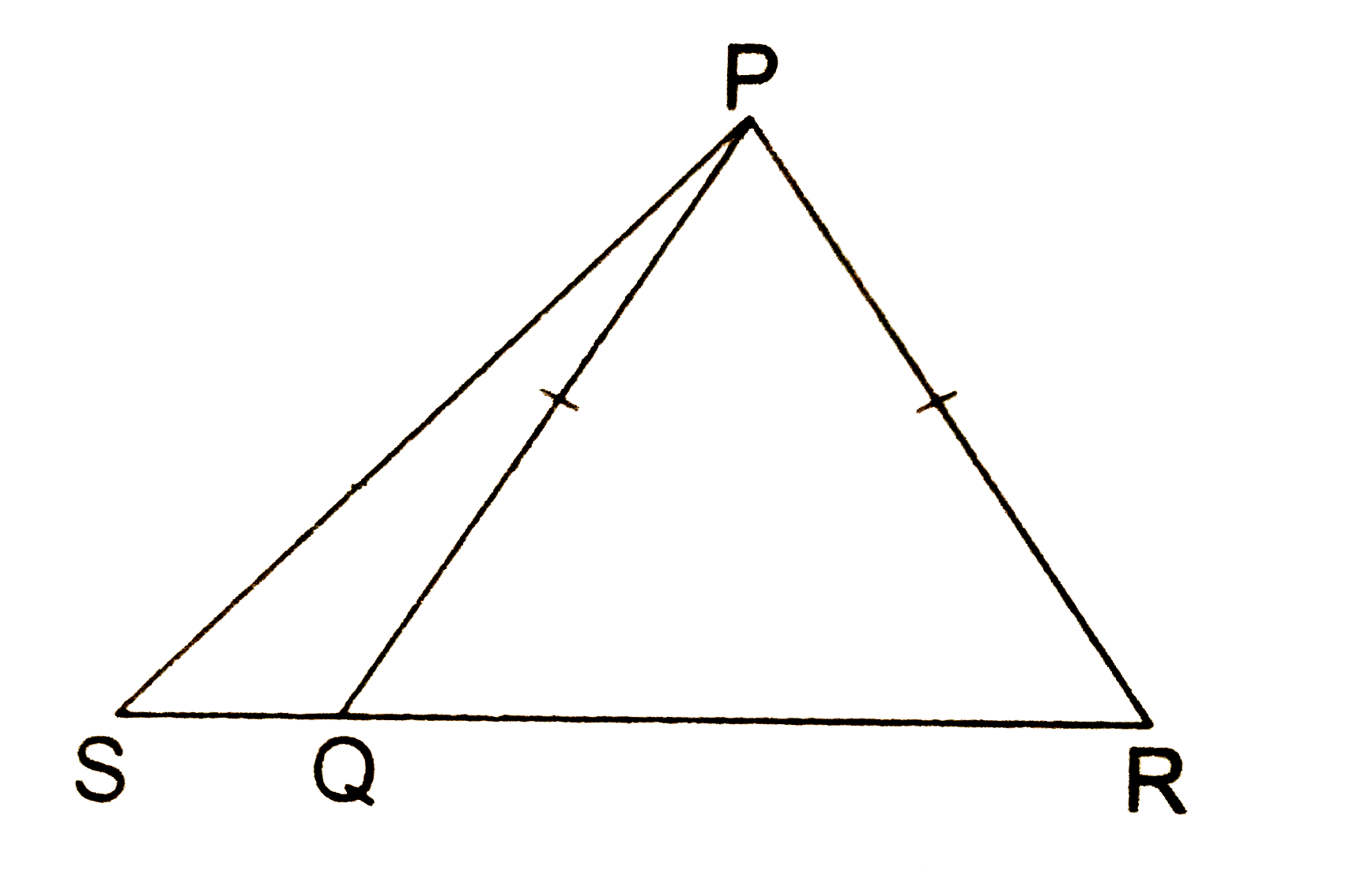 View Solution
View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
View SolutionIn the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).
 View Solution
View SolutionPQRS is a parallelogram. PS is produced to M, so that SM = SR and MR produced meets PQ produced at N. Prove that QN = QR.
View SolutionPQRS is a parallelogram. PS is produced to M, so that SM = SR and MR produced meets PQ produced at N. Prove that QN = QR.
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
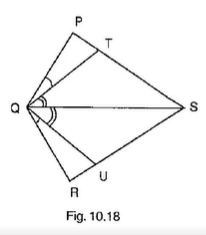 View Solution
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
 View Solution
View Solution

