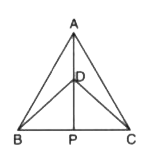
The given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that:
ΔABD=ΔACD
(ii) ΔABP=ΔACP
(iii) AP bisects ∠BDC
(iv) AP is perpendicular bisector of BC.
Step by step video & image solution for The given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that: Delta ABD = Delta ACD (ii) Delta ABP = Delta ACP (iii) AP bisects angle BDC (iv) AP is perpendicular bisector of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Inequalities
Explore 5 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Mid-point and intercept theorem
Explore 11 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:logrithms
Explore 20 Videos
- CHAPTER REVISION (STAGE 2) Book:ICSEChapter:CHAPTER REVISION (STAGE 2) Exercise:DISTANCE FORMULA
Explore 12 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:DISTANCE FORMULA
Explore 11 Videos
Similar Questions
ΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionABC is an equilateral triangle .If AD bisects angle A, Prove that AD is perpendicular bisector of BC .
View SolutionConstruct two isosceles triangles ABC and DBC, with common base BC and the points A and D on opposite sides of BC, given that BC = 8 cm, AB = AC = 4.5 cm, and DB = DC = 5 cm.
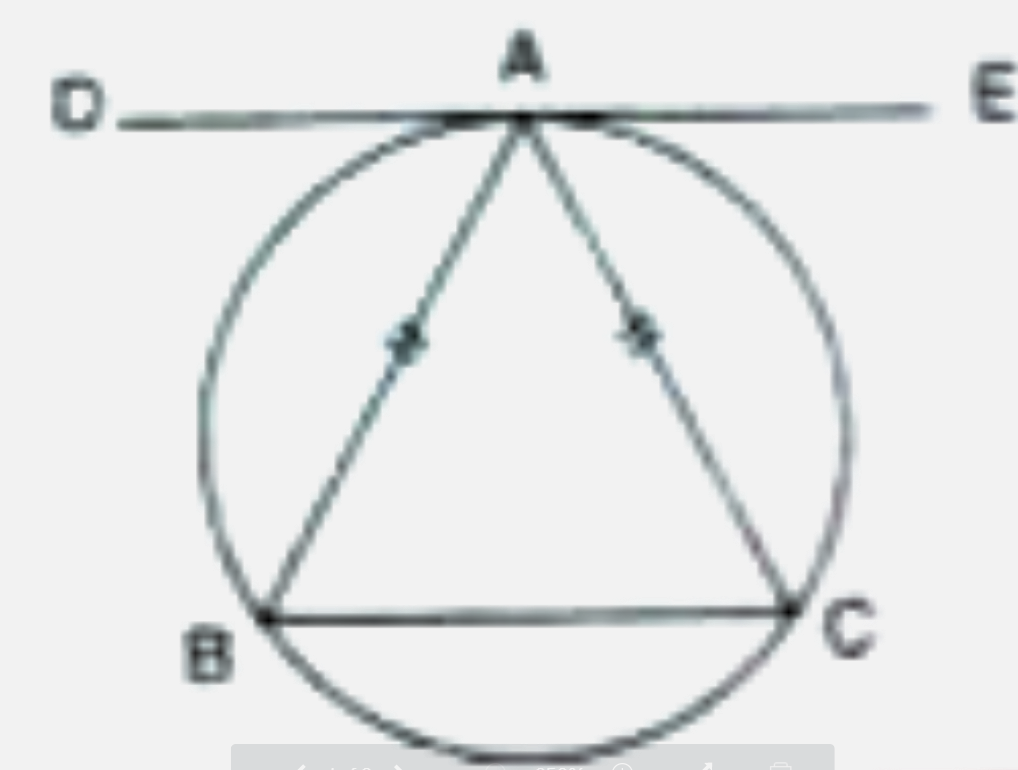
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
ΔABP≅ΔACP
View SolutionInΔABC,AB=ACandD is a piont in side BC such that AD bisect angle BAC.
Show that AD is perpendicular bisector of side BC.
View SolutionThe given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View SolutionIn a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) ΔABDandΔECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
View SolutionThe given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.
View Solution