Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
 Solution in Tamil
Solution in Tamil
1.1×10−4m
1.8×10−4m
1.3×10−4m
1.5×10−4m
The correct Answer is:C
Y=F.lA.Δl,Δl=F.lA.Y
For Brass,
Δl=6×9.8N×1mπ(0.125×10−2m)2×(9.1×1010Nm−2)
=1.3×10−4m
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS ( VERY SHORT ANSWER QUESTIONS )36videos
PROPERTIES OF MATTER
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (SHORT ANSWER QUESTIONS )48videos
PROPERTIES OF MATTER
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - EVALUTION TEXTBOOK QUESTIONS & ANSWERS (NUMERICAL PROBLEMS )20videos
PROPERTIES OF MATTER
- BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( CONCEPTUAL QUESTIONS.)24videos
OSCILLATIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - QUESTION PAPER MARCH 2019EXERCISE - Part- IV23videos
QUESTION PAPER MARCH 2019
Similar Questions
What is a deforming force?
03:55View SolutionWhat do you know about restoring force?
02:14View SolutionA cappilary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made (23) of its previous value, then compute the height up to which water will rise in the new capillary ?
05:35View SolutionCan a motion be periodic and not oscillatory ?
09:42View SolutionThe force F acting on a body moving in a circular path depends on mass of the body (m) velocity(v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method (k=1)
06:20View SolutionTwo wires of diameter 0.25 cm , one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5 m and that of brass is 1.0 m . Young's modulus of steel is 2.0 xx 10^(11) Pa and that of brass is 1.0 xx 10^(11) Pa. Compute the ratio of elongations of steel and brass wires. (/_\l_("steel"))/(/_\l_("brass"))=?
04:33View SolutionCompute the elongation of the steel wire and brass wire in the given Given unloaded length of steel wire = 2.0 m, unloaded length of brass wire = 1.0m. Area of cross-section of each wire = 0.049 cm^2. Y_(steel) = 2xx10^(11)Pa and Y_(Brass) = 0.90 xx 10^(11)P_a , g = 9.8 ms^(-2)
View Solution0.25 cm व्यास कि दो तार, जिनमे एक इस्पात का तथा दूसरा पीतल का है, चित्र के अनुसार भारित है। बिना भार लटकाये इस्पात तथा पीतल के तारो की लम्बाईयाँ क्रमश: 1.5 मीटर तथा 1.0 मीटर है। यदि इस्पात तथा पीतल के यंग गुणांक 2.0×1011 Pa तथा 0.91×1011 Pa हो तो इस्पात तथा पीतल के तारो में विस्तार की गणना कीजिए।
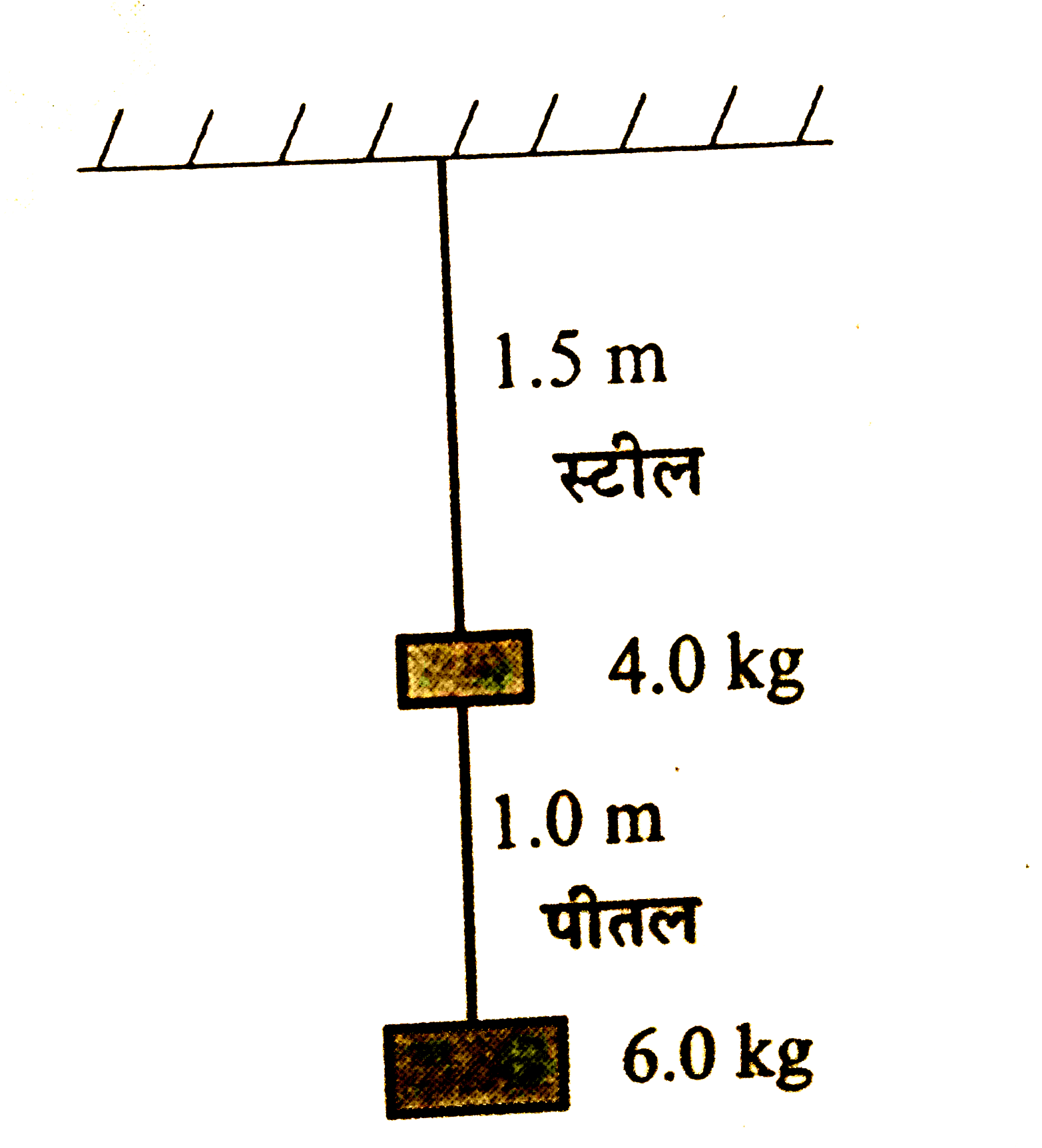 03:34View Solution
03:34View Solution0.25 सेमी व्यास के दो तार , जिनमे एक इस्पात का तथा दूसरा पीतल का है , चित्र के अनुसार भारित है । बिना भार लटकाये इस्पात तथा पीतल के तारो की लम्बाईयाँ क्रमशः 1.5 मीटर तथा 1.0 मीटर है । यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः 2.0×1011 तथा 0.91×1011 हो , तो इस्पात तथा पीतल के तारो में विस्तार की गणना कीजिए ।
 03:36View Solution
03:36View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
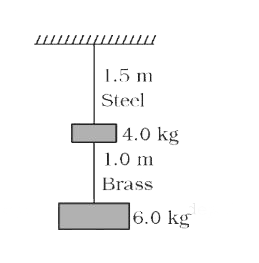 07:22View Solution
07:22View SolutionIf the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
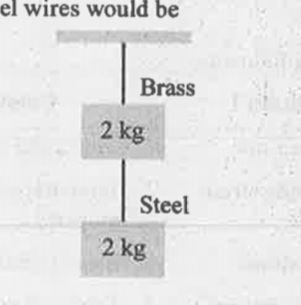 06:29View Solution
06:29View SolutionThe Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
07:10View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
05:11View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
03:03View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
 05:52View Solution
05:52View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.
 04:00View Solution
04:00View Solution

