The ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
![The ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_19Y_SP_17_E01_038_Q01.png)
Solution in Telugu
4a7bc
7bc4a
4bc7a
7a4bc
The correct Answer is:C
Let the ratio of length be a ratio of area be b
Ratio of Young .s modulus be c
we know that ,
Y=F/AΔL/L
∴ΔL=FLAY
ΔLsΔLB=(FSFB)(LSLB)(ABAS)(YBYS)
=74×(a)(1b)×(1c)
ΔLSΔLB=7a4bc
ΔLBΔS=4bc7a
Topper's Solved these Questions
- BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)EXERCISE - PHYSICS39videos
AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)
- BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1)EXERCISE - Physics40videos
AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1)
Similar Questions
IF the charge of electron c , mass of electron m, speed of light in vaccum c and Planck's constant h are taken as fundamental quantities. Then the permeability of vaccum μ0 can be expressed as
04:08View SolutionAssertion (A) Energy per unit volume and angular momentum can be added dimensionally.
Reason (R ) Physical quantities having same dimension can be added or subtracted.02:32View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a, b and c respectively then the corresponding ratio of increase in their lengths is
05:32View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
04:38View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
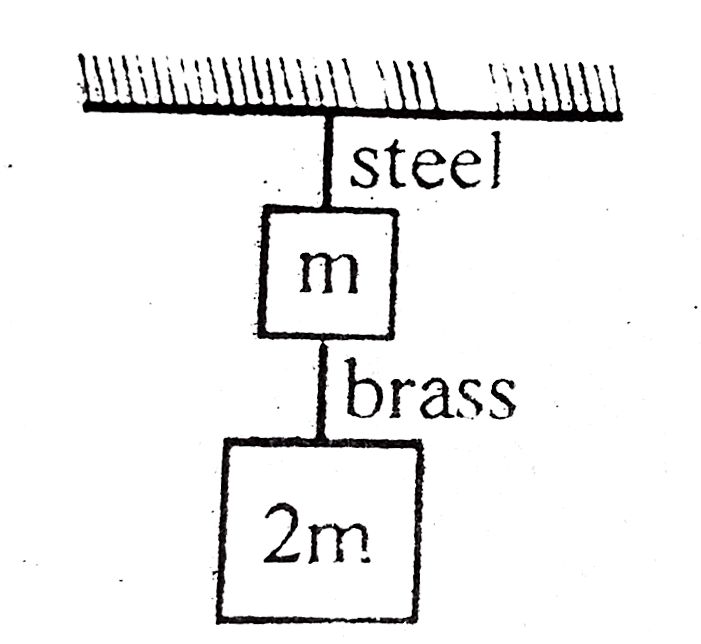
02:46View SolutionIf the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be
04:33View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
View SolutionIf the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
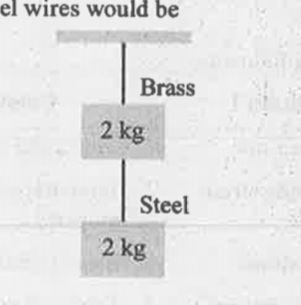
06:29View SolutionThe Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
07:10View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.
02:32View Solutionचित्र में दिखाए गए स्टील तथा पीतल के तारों की लम्बाइयों, त्रिज्याओं तथा यंग प्रत्यास्थता गुणांकों में अनुपात क्रमशः a,b तथा c हैं। पीतल के तार की लम्बाई में वृद्धि तथा स्टील के तार की लम्बाई में वृद्धि में अनुपात होगा
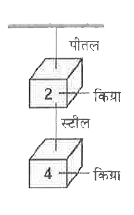
03:26View SolutionThe Young's modulus of steel is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of:
05:34View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of
03:18View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
02:25View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a, b and c respectively then the corresponding ratio of increase in their lengths is
03:10View Solution