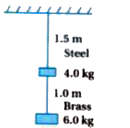
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
 Solution in Gujrati
Solution in Gujrati
For steel wire,
F _(B) = 6 xx 9.8 Nl _(R) = (F _(B) L _(B))/( pi r _(B) ^(2) Y _(B))= (6 xx 9.8 xx 1 )/( 3.14 xx (0.125 xx 10 ^(-2)) ^(2) xx 0.91 xx 10 ^(11))l _(B) = 1217 xx 10 ^(-7)therefore l _(B) = 1.317 xx 10 ^(-4) mtherefore l _(B) ~~ 1.3 x 10 ^(-4) m
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-C66videos
MACHANICAL PROPERTIES OF SOLIDS
- BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-D29videos
MACHANICAL PROPERTIES OF SOLIDS
- BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-A TRY YOURSELF (VSQs)40videos
MACHANICAL PROPERTIES OF SOLIDS
- BOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D1videos
LAW OF MOTION
- BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - QUESTION PAPER (SECTION -C)3videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
What is elasticity ? What is plastic body and plasticity?
03:55View SolutionModulus of rigidity of an ideal liquid is ......
02:14View SolutionWhat are solid bodies composed ?
05:35View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
09:42View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm . If the amount of glycerine collected per second at one is 4.0×10−3kgs−1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine =1.3×10103kgm−3 and viscosity of glycerine =0.83 Pa s). [ you may also like to check if the assumption of laminar flow in the tube is correct]
06:20View SolutionTwo wires of diameter 0.25 cm , one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5 m and that of brass is 1.0 m . Young's modulus of steel is 2.0 xx 10^(11) Pa and that of brass is 1.0 xx 10^(11) Pa. Compute the ratio of elongations of steel and brass wires. (/_\l_("steel"))/(/_\l_("brass"))=?
04:33View SolutionCompute the elongation of the steel wire and brass wire in the given Given unloaded length of steel wire = 2.0 m, unloaded length of brass wire = 1.0m. Area of cross-section of each wire = 0.049 cm^2. Y_(steel) = 2xx10^(11)Pa and Y_(Brass) = 0.90 xx 10^(11)P_a , g = 9.8 ms^(-2)
View Solution0.25 cm व्यास कि दो तार, जिनमे एक इस्पात का तथा दूसरा पीतल का है, चित्र के अनुसार भारित है। बिना भार लटकाये इस्पात तथा पीतल के तारो की लम्बाईयाँ क्रमश: 1.5 मीटर तथा 1.0 मीटर है। यदि इस्पात तथा पीतल के यंग गुणांक 2.0×1011 Pa तथा 0.91×1011 Pa हो तो इस्पात तथा पीतल के तारो में विस्तार की गणना कीजिए।
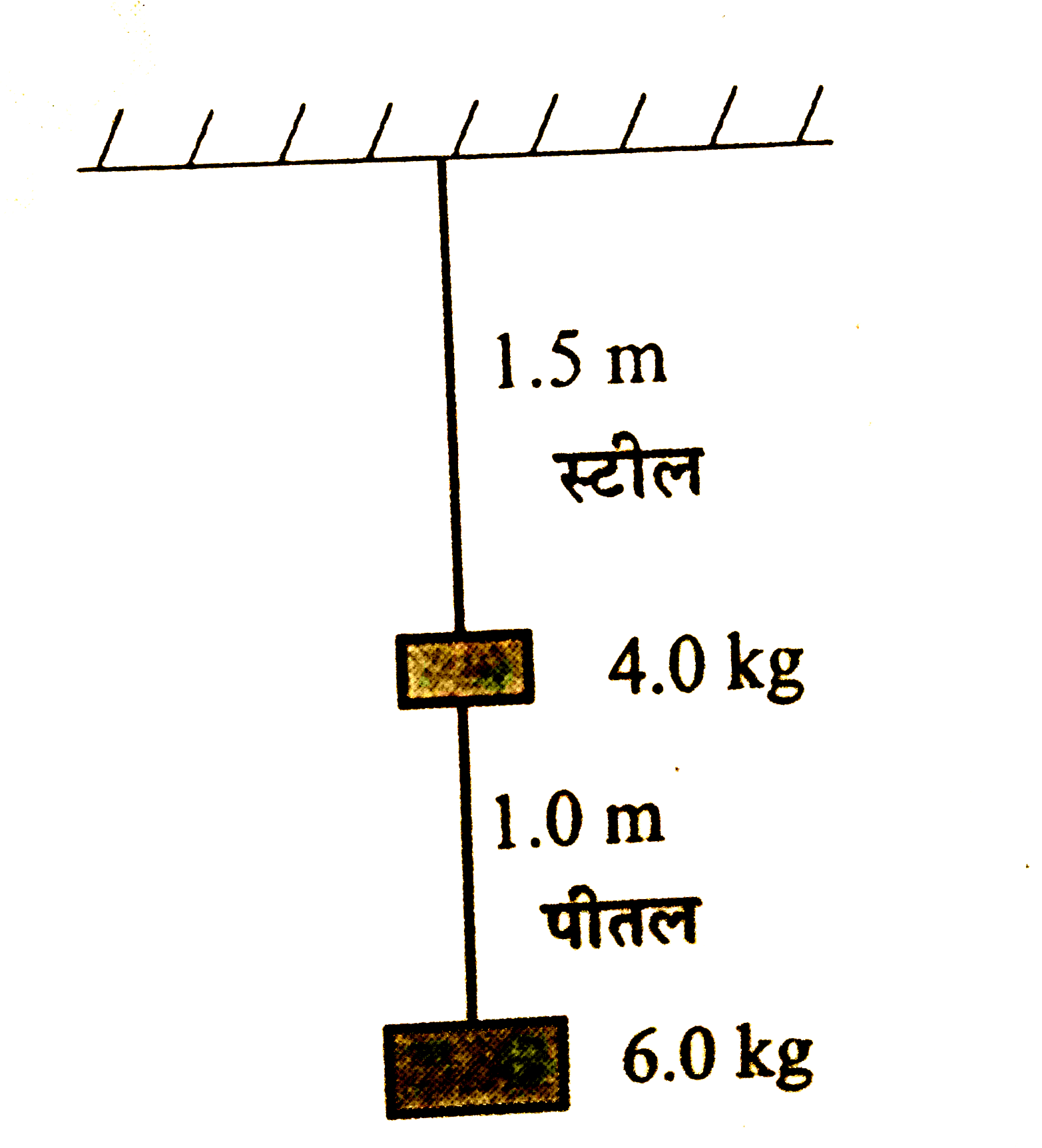 03:34View Solution
03:34View Solution0.25 सेमी व्यास के दो तार , जिनमे एक इस्पात का तथा दूसरा पीतल का है , चित्र के अनुसार भारित है । बिना भार लटकाये इस्पात तथा पीतल के तारो की लम्बाईयाँ क्रमशः 1.5 मीटर तथा 1.0 मीटर है । यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः 2.0×1011 तथा 0.91×1011 हो , तो इस्पात तथा पीतल के तारो में विस्तार की गणना कीजिए ।
 03:36View Solution
03:36View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
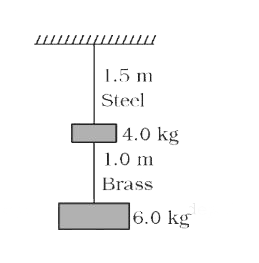 07:22View Solution
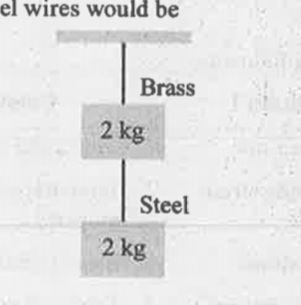
07:22View SolutionIf the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
 06:29View Solution
06:29View SolutionThe Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
07:10View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
03:03View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
05:52View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
 04:00View Solution
04:00View Solution

