A solid spher of mass m1 density ρ1 radius R1 and a solid cone of mass m2 density ρ2. Radius R2, are arranged as shown in the figure. The centre of mass is located at
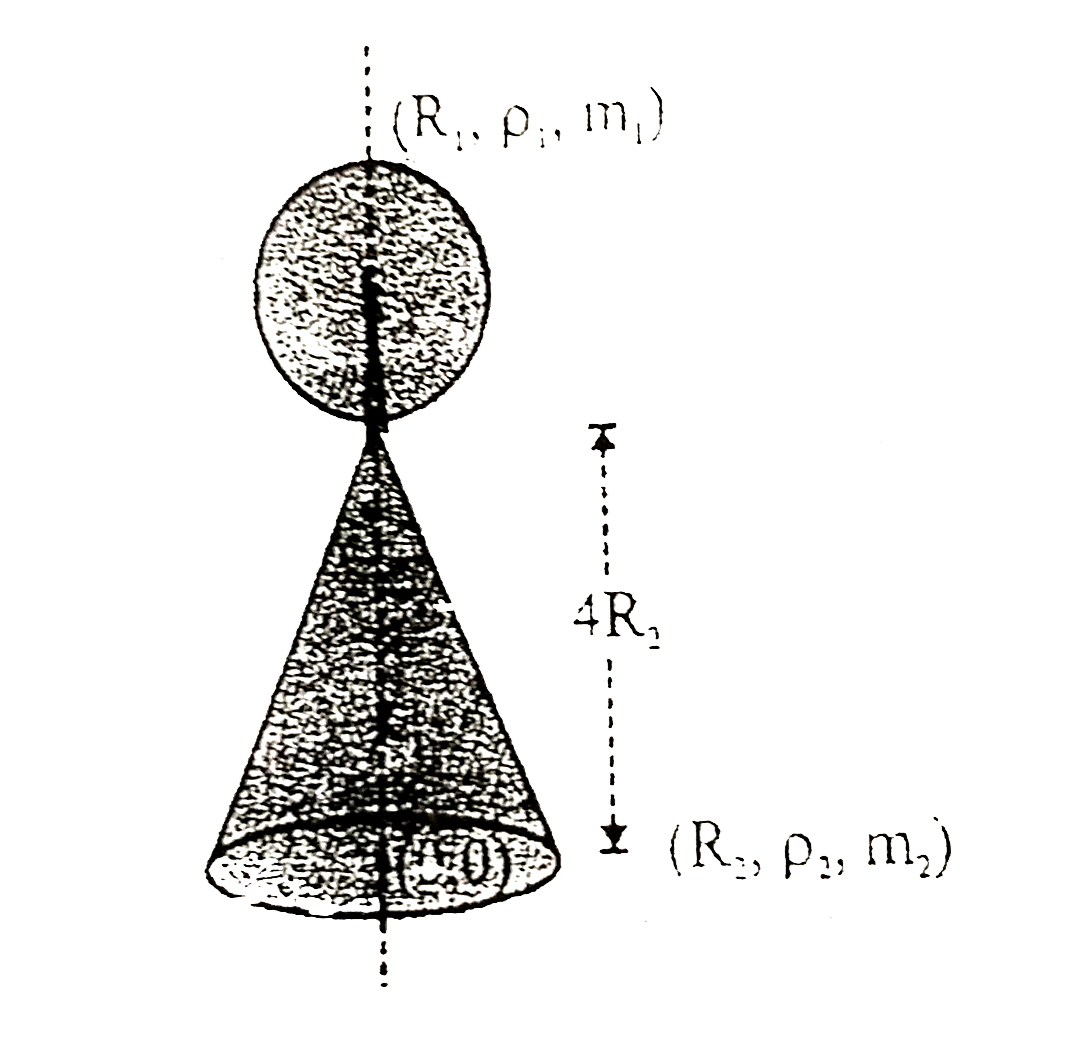
(0, 3R) if m1=m2=m and R1=R2=R
(0, 3R) if ρ1=ρ2 and R1=R2=R
(0,11R3) if ρ1=2ρ2 and R1=R2=R
always at (0,4R2)
The correct Answer is:A, B, C
(A) yCOM=m×h4+m(h+R1)2m
yCOM=m×(R)+m(5R)2m
yCOM=3R
xCOM=0
(B) ρ1=ρ2=ρ
m1=ρ43πR3
m2=ρ×π(R)2(4R)3=43πR2ρ
again m1=m2 & R1=R2
so same as option (A)
(C ) Let ρ2=ρ, then ρ1=2ρ
m1=(2ρ)43πR3=8ρπR33
m2=(ρ)(πR2)(4R)3=43πρR3
yCOM=m1(4R+R)+m2(4R4)m1+m2
yCOM=(83ρπR3)(5R)+43πρR3(R)83ρπR3+43πρR3
yCOM=403ρπR4+43ρπR412ρπR33
yCOM=44ρπR4312ρπR33=11R3
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART B
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART A
12 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (C )
15 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Two stars of mass M1&M2 are in circular orbits around their centre of mass The star of mass M1 has an orbit of radius R1 the star of mass M2 has an orbit of radius R2 (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R1/R2=M2/M1
(b) Explain why the two stars have the same orbital period and show that the period
T=2π(R1+R2)3/2√G(M1+M2) .
View SolutionTwo stars of mass M1&M2 are in circular orbits around their centre of mass The star of mass M1 has an orbit of radius R1 the star of mass M2 has an orbit of radius R2 (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R1/R2=M2/M1
(b) Explain why the two stars have the same orbital period and show that the period
T=2π(R1+R2)3/2√G(M1+M2) .
View Solution
Knowledge Check
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20If two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2roh1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionOn to a sphere of radius R/2 and density P2 with centre at C2 a second solid sphere is moulded with density p1 radius R and centre C1. Find the force experienced by a point mass m at point P at a distance y from the combination as shown.
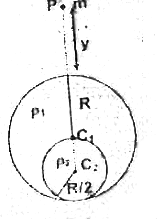
View SolutionOn to a sphere of radius R/2 and density P2 with centre at C2 a second solid sphere is moulded with density p1 radius R and centre C1. Find the force experienced by a point mass m at point P at a distance y from the combination as shown.
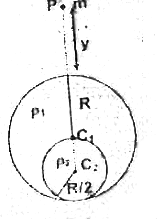
View SolutionA solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View SolutionThe moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
View SolutionThe moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
View Solution
