A uniform thin rod AB of mass M and length l stands at the edge of a frictionless table as shown in the figure. A particle of mass m = M/2 flying horizontally with a velocity $v_{0}$ strikes the rod at its top edge A and sticks to it. The rod is immediately driven off the table. Determine

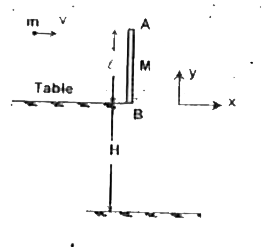
(a) velocity of centre of mass of the system (rod + particle) just after collision between M and m.
(b) position of centre of mass of the system. (Take edge of table at origin).
(c) angular velocity of the system about centre of mass.
(d) the position of the centre of mass of the system when it rotates by $180^{\circ}$ (Take $v_{0} = π$ m/s and l = 1 m)
(e) at t = 1.5 sec, rod hits the horizontal plane at depth H below the table. Find H and coordinate of edge B of the rod just before striking the ground. (take g = 10 $m / s^{2}$ )

Text Solution

Verified by Experts

(a) Applying conservation of momentum.
$m v_{0} = (M + m) v$
$\Rightarrow v = \frac{M}{2} \frac{v_{0}}{(3 M / 2)} = \frac{v_{0}}{3} \Rightarrow v = \frac{v_{0}}{3}$

(b) Centre of mass is taking as lower edge in contact with the table as origin
$y = (\frac{M l}{2} + \frac{M l}{2}) / \frac{3 M}{2} = \frac{2 M l}{3 M} = \frac{2 l}{3}$
(c) Applying conservation of angular momentum of the system about C,
$\frac{M}{2} v_{0} \frac{l}{3} = I ω = [\frac{M l^{2}}{12} + M {(\frac{l}{6})}^{2} + \frac{M}{2} {(\frac{l}{3})}^{2}] ω$
$\Rightarrow \frac{M}{2} v_{0} \frac{l}{3} = \frac{M l^{2}}{6} ω$
$\Rightarrow ω = \frac{v_{0}}{l}$

(d) $ω t = π (for θ = 180^{\circ})$
$t = \frac{π}{ω}$
$t = \frac{π l}{v_{0}}$
$∴ t = 1 sec$
$∴$ x-coordinate difference x = vt = $\frac{v_{0}}{3} .1 = \frac{π}{3}$ m and
y-coordinate = $(\frac{2}{3} - \frac{1}{2} \times 10 \times 1^{2}) = - \frac{13}{3} m$
(e) $θ = ω t = \frac{v_{0}}{l} \times 1.5 \Rightarrow θ = \frac{3 π}{2}$
$∴$ Rod hits the plane horizontally.
$\frac{2 l}{3} + H = \frac{1}{2} g t^{2} = 5 \times {(\frac{3}{2})}^{2} \Rightarrow H = 11.25 - \frac{2}{3} = 10.58 m$
$x_{c m} = v t = \frac{π}{3} \times \frac{3}{2} = \frac{π}{2} m$
x-coordinate of B $= (\frac{π}{2} - \frac{2}{3})$ and y-coordinate of B = - 10.58 m

Updated on:21/07/2023