A uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod is released from rest in the position shown by slightly displacing it clockwise. Find the hinge reaction at the axis of rotation at the instant the rod turns through (a) 90∘ (b) 180∘

Applying law of conservation of energy
12Iω2=mgl2(1−cosθ)
Torque about hinge point is
mgl2sinθ=ml23α
aT=(l/2)α
αN=ω2(l/2)
Nx=mω2l2sinθ−ml2αcosθ
Ny−mg=−ml2αsinθ−mω2l2cosθ
Putting the value of, θ=90∘ in equation (1), (2), (3), (4)
Nx=3mg2(←)
Ny=mg4(↑⏐)
Putting θ=180∘
Nx=0
Ny=4mg(↑⏐)
(a) Nx=3mg2←,Ny=mg4↑⏐
⏐⏐
(b) Nx=0,Ny=4mg↑⏐
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)14videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSERTION REASONING TYPE1videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - IV2videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type6videos
PHYSICS PART2
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
Similar Questions
A uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
 View Solution
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView Solution
Knowledge Check
- Question 1 - Select One

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθ - Question 2 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation

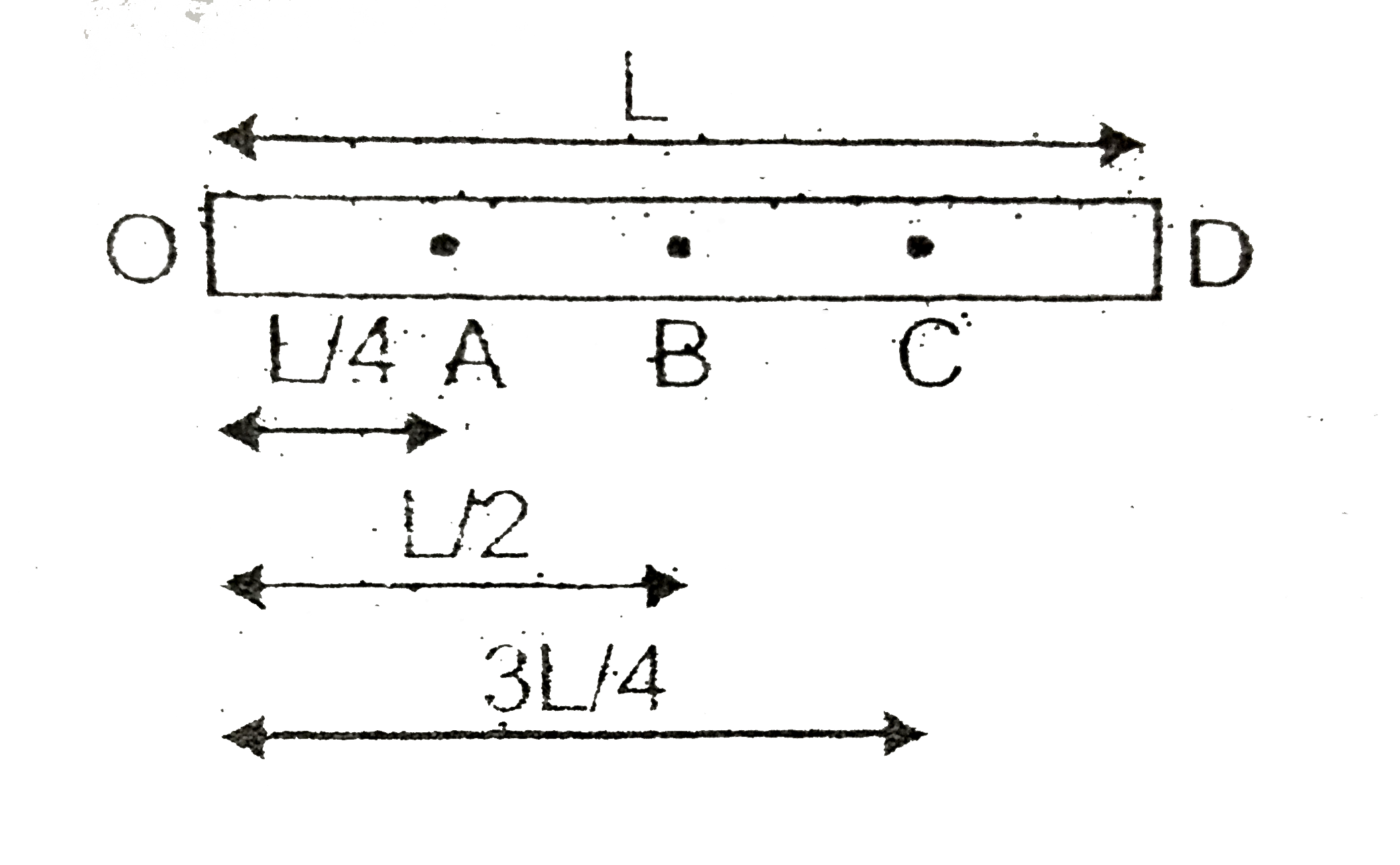
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
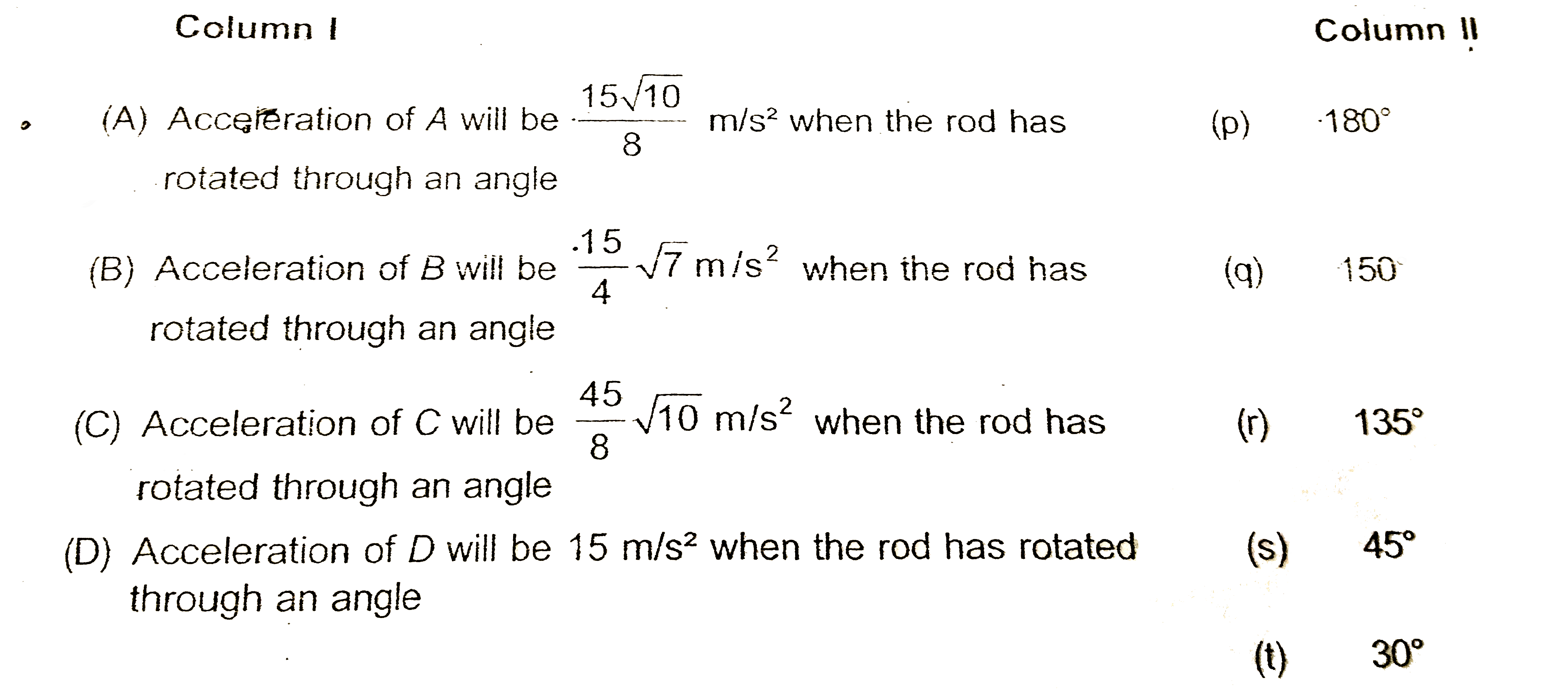 View Solution
View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II

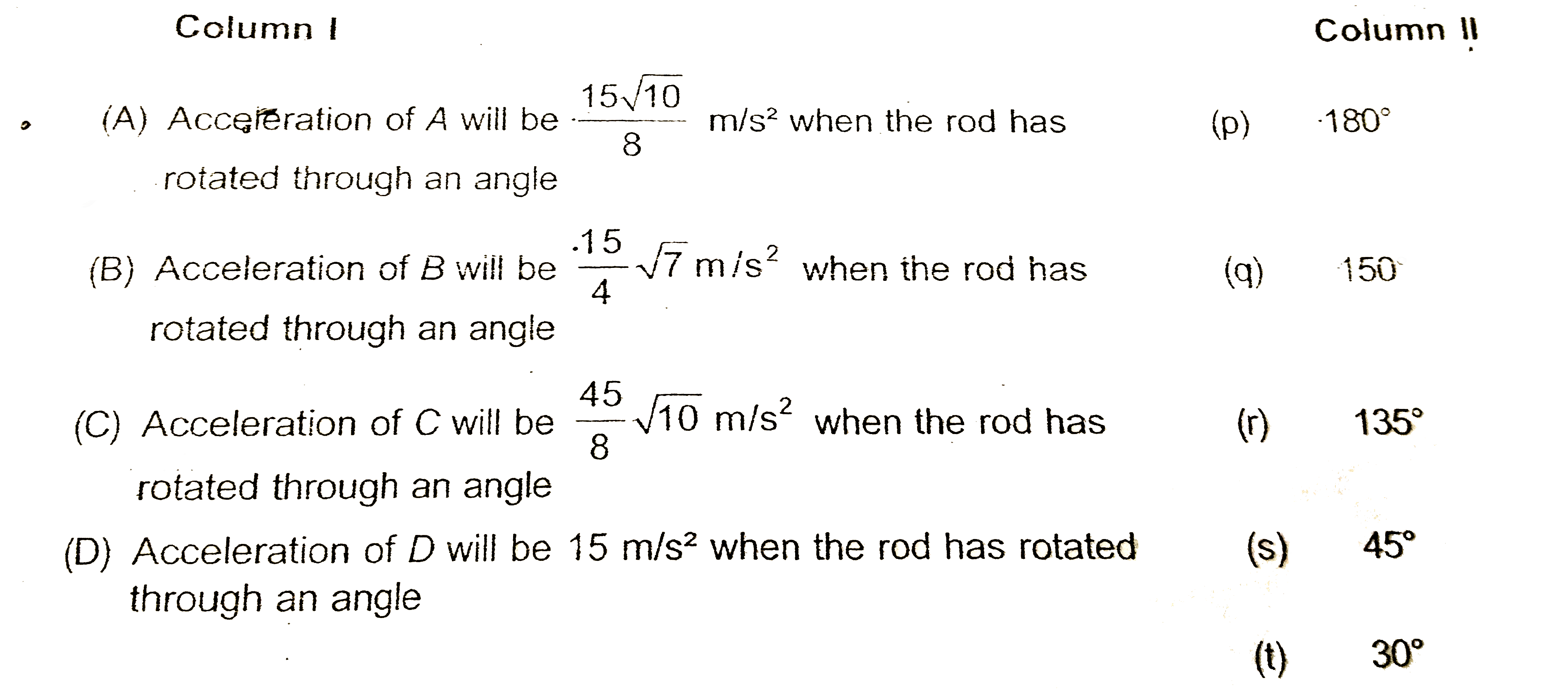 View Solution
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?
 View Solution
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?
 View Solution
View SolutionA uniform rod is rotating about a horizontal axis as shown. The rod is hinged at one of the ends. The rod is released from a vertical position by slightly pushing it. As the rod moves from A to B
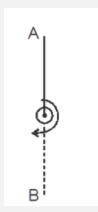 View Solution
View Solution

