Find the magnetic force on a short magnet of magnetic dipole moment M2 due to another short magnet of magnetic dipole moment M1.

To find the magnetic force we will use the formula of B due to a magnet.We will also assume m and −m as pole strengths of N and S of M2.Also length of M2 as 2a.B1 and B2 are the strengths of the magnetic field due to M1 at +m and −m respectively.They experience magnetic forces F1 and F2 as shown.
F1=2(μ04π)M1(r−a)3m
and F2=2(μ04π)M1(r−a)3m
∴Fres=F1−F2=2(μ04π)M1m[(1(r−a)3)−(1(r+a)3)]
=2(μ04π)M1mr3[(1−ar)−3−(1+ar)−3]
By using acceleration, Binomial expansion, and neglecting terms of high power we get
Fres=2(μ04π)M1mr3[1+3ar−1+3ar]
=2(μ04π)M1mr36ar
=2(μ04π)M13M2r4
=6(μ04π)M1M2r4
Direction of Fres is towards right.
Alternative Method
=B(μ04π)2M1r3⇒dBdr=−μ04π×6M1r4
F=−M2×dBdr⇒F=(μ04π)6M1M2r4

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
81 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Knowledge Check
Magnetic dipole moment is a
AScalar quantityBVector quantityCConstant quantityDNone of theseA bar magnet of length l and magnet dipole moment M is bent in the form of an arc. The new magnetic dipole moment is
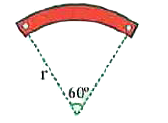 A3πMB2πMCM2DM
A3πMB2πMCM2DMThe magnetic potential at any point due to short magnetic dipole is
AV=μ04πMrBV=μ04πMr2CV=±μ04πMr2DV=0
Magnetic Dipole Moment || Torque
View SolutionFollowing figures show the arrangement of bar magnets in different configurations. Each magnet has magnetic dipole moment (m). Which configuration has highest value of magnetic dipole moment?
View SolutionFollowing figures show the arrangement of bar magnets in different configurations. Each magnet has magnetic dipole moment (m). Which configuration has highest value of magnetic dipole moment?
View SolutionFollowing figures show the arrangement of bar magnets in different configurations. Each magnet has magnetic dipole moment (m). Which configuration has highest value of magnetic dipole moment?
View SolutionFollowing figures show the arrangement of bar magnets in different configuration . Each magnet has magnetic dipole moment m. Which configuration has highest net magnetic dipole moment ?
View Solution

