A pendulum bob has mass 4 mg and carrieas a charge 2×10−9 coulomb. It hangs in equilibrium from a massless thread of length 50 cm whose other end is fixed to a vertical wall. A horizontal electtic field of inetensity 20000 V/m exists in space. Calculate
a. Angle made by the thread with the vertical
b. Tension in the thread
To solve the problem step by step, we will calculate the angle made by the thread with the vertical and the tension in the thread.
Given Data:
- Mass of the pendulum bob, m=4mg=4×10−6kg
- Charge on the bob, q=2×10−9C
- Length of the thread, L=50cm=0.5m
- Electric field intensity, E=20000V/m
- Acceleration due to gravity, g=10m/s2
Step 1: Calculate the forces acting on the bob
1. Weight of the bob (mg):
W=mg=4×10−6kg×10m/s2=4×10−5N
2. Electric force (F_e):
Fe=qE=2×10−9C×20000V/m=4×10−5N
Step 2: Set up the equations for equilibrium
At equilibrium, the vertical component of tension balances the weight of the bob, and the horizontal component of tension balances the electric force.
1. Vertical component:
Tcosθ=mg(1)
2. Horizontal component:
Tsinθ=qE(2)
Step 3: Divide equation (2) by equation (1)
TsinθTcosθ=qEmg
This simplifies to:
tanθ=qEmg
Step 4: Substitute the values
tanθ=2×10−9×200004×10−5
Calculating this:
tanθ=4×10−54×10−5=1
Step 5: Calculate the angle
Since tanθ=1,
θ=45∘
Step 6: Calculate the tension in the thread
Using either equation (1) or (2), we can find the tension T. Let's use equation (1):
T=mgcosθ
Substituting the values:
T=4×10−5cos45∘=4×10−51√2=4×10−5×√2
Calculating this gives:
T=4√2×10−5N≈5.66×10−5N
Final Answers:
a. The angle made by the thread with the vertical is 45∘.
b. The tension in the thread is approximately 5.66×10−5N.
- Mass of the pendulum bob, m=4mg=4×10−6kg
- Charge on the bob, q=2×10−9C
- Length of the thread, L=50cm=0.5m
- Electric field intensity, E=20000V/m
- Acceleration due to gravity, g=10m/s2
1. Weight of the bob (mg):
W=mg=4×10−6kg×10m/s2=4×10−5N
Fe=qE=2×10−9C×20000V/m=4×10−5N
At equilibrium, the vertical component of tension balances the weight of the bob, and the horizontal component of tension balances the electric force.
Tcosθ=mg(1)
Tsinθ=qE(2)
TsinθTcosθ=qEmg
This simplifies to:
tanθ=qEmg
tanθ=2×10−9×200004×10−5
Calculating this:
tanθ=4×10−54×10−5=1
Since tanθ=1,
θ=45∘
Using either equation (1) or (2), we can find the tension T. Let's use equation (1):
T=mgcosθ
Substituting the values:
T=4×10−5cos45∘=4×10−51√2=4×10−5×√2
Calculating this gives:
T=4√2×10−5N≈5.66×10−5N
a. The angle made by the thread with the vertical is 45∘.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EVALUATE YOURSELF-110videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EVALUATE YOURSELF-29videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)17videos
DUAL NATURE
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)23videos
ELECTRO MAGNETIC INDUCTION
Similar Questions
A pendulum bob of mass 80mg and carrying a charge of 2×10−8C is at rest in a uniform, horizontal electric field of 20k Vm−1. Find the tension in the thread.
View SolutionA pendulum bob of mass 80mg and carrying a charge of 2×10−4 coulomb is at rest in a uniform horizontal electric field of 20kVm.The tension in the thread of the pendulum is x times10−4 N.Find value of x?
View Solution
Knowledge Check
- Question 1 - Select One
The bob of a simple pendulum has mass 2g and a charge of 5.0μC. It is at rest in a uniform horizontal electric field of intensity 2000V/m. At equilibrium, the angle that the pendulum makes with the vertical is: (take g=10m/s2)
Atan−1(2.0)Btan−1(0.2)Ctan−1(5.0)Dtan−1(0.5) - Question 2 - Select One
A block of mass 5kg is suspended by a massless rope of length 2 m from the ceiling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
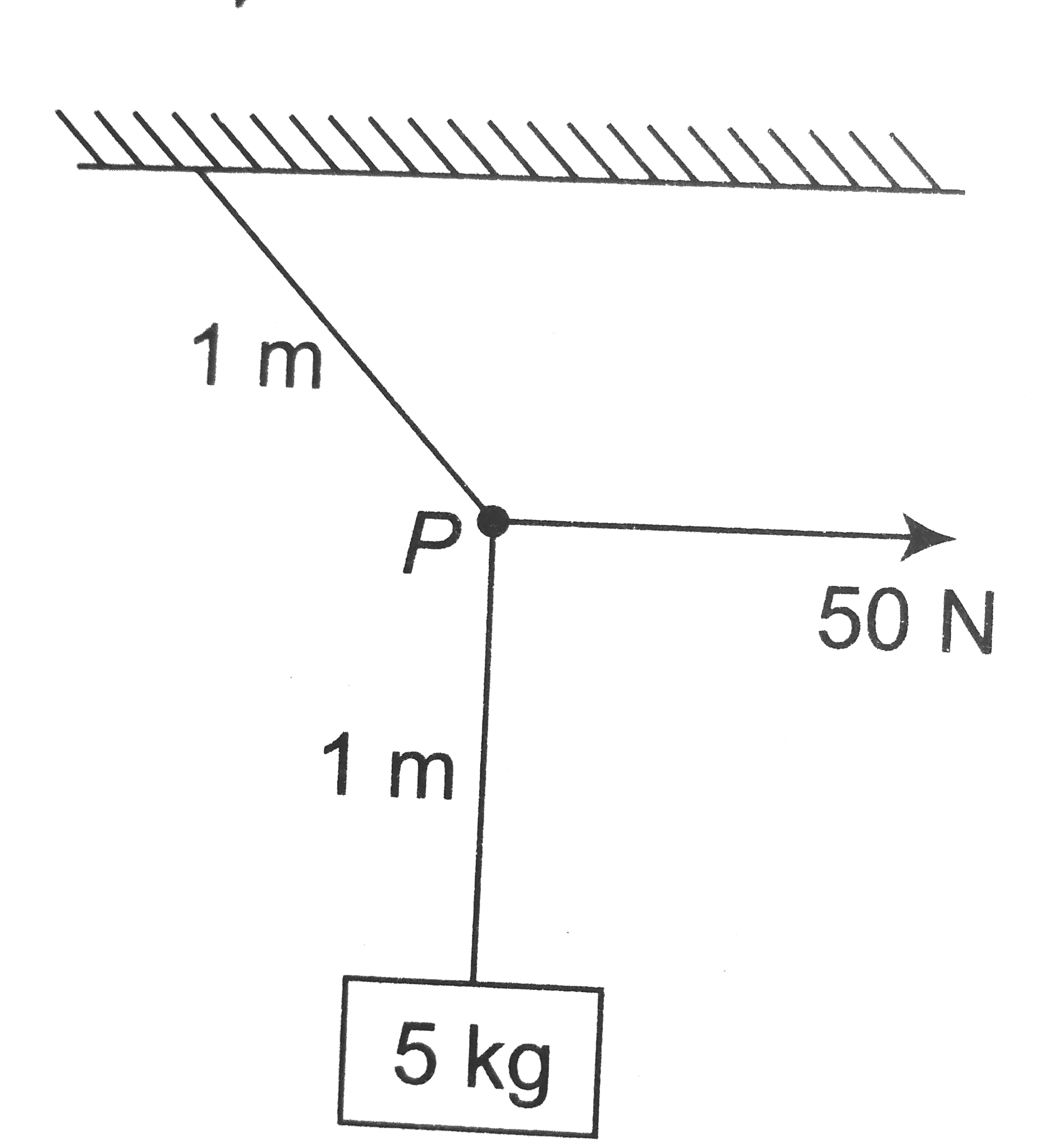 A30∘B40∘C60∘D45∘
A30∘B40∘C60∘D45∘ - Question 3 - Select One
The bob of a pendulum of mass 8μg carries an electric charge of 39.2×10−10 coulomb in an electric field of 20×103 volt/meter and it is at rest. The angle made by the pendulum with the vertical will be
A27∘B45∘C87∘D127∘
A pendulum bob of mass 80 mg and carrying charge of 3×10−8C is placed in an horizontal electric field. It comes to equilibrium position at an angle of 37∘ with the vertical. Calculate the intensity of electric field. (g = 10m/s2 )
View SolutionA particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionTwo small spheres, each of mass 0.1 gm and carrying same charge 10−9C are suspended by threads of equal length from the same point. If the distance between the centres of the sphere is 3 cm, then find out the angle made by the thread with the vertical. (g=10m/s2) & tan−1(1100)=0.6º
View SolutionA pith ball carrying a charge of 3×10−10C is suspended by an insulated thread of length 50cm.When a uniform electric filed is applied in a horizontal direction , the ball is found to deflect by 2cm from the vertical. If the mass of the ball is 0.5gm , the intensity of the electric field is :
View SolutionA particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/s2)
View Solution

