A square loop of side 2a and carrying current I is kept in xz plane with its centre at origin. A long wire carrying the same cruurent I is placed parallel to z - axis and passing through point (0,b,0), (b >>a). The magnitude of troque on the loop about z - axis will be :
2μ0I2a2πb
2μ0I2a2bπ(a2+b2)
μ0I2a2b2π(a2+b2)
μ0I2a22πb
To find the magnitude of the torque on the square loop about the z-axis, we will follow these steps:
Step 1: Determine the Magnetic Moment (M) of the Square Loop
The magnetic moment M of a current-carrying loop is given by the formula:
M=I⋅A
where I is the current flowing through the loop and A is the area of the loop.
Given that the side of the square loop is 2a, the area A is:
A=(2a)2=4a2
Thus, the magnetic moment M becomes:
M=I⋅4a2=4a2I
Step 2: Calculate the Magnetic Field (B) due to the Long Wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
In this case, the distance r from the wire to the center of the square loop is b (since the wire is at point (0,b,0) and the loop is centered at the origin).
Thus, the magnetic field at the position of the loop is:
B=μ0I2πb
Step 3: Determine the Direction of the Magnetic Moment (M)
The current in the loop flows in an anti-clockwise direction when viewed from the positive z-axis. Therefore, the direction of the magnetic moment M is in the positive y-direction:
M=4a2I^j
Step 4: Determine the Direction of the Magnetic Field (B)
Using the right-hand rule, if the current in the wire flows upwards (in the positive z-direction), the magnetic field at the location of the loop (which is in the xz-plane) will be directed in the positive x-direction:
B=μ0I2πb^i
Step 5: Calculate the Torque (τ) on the Loop
The torque τ on the loop is given by the cross product of the magnetic moment M and the magnetic field B:
τ=M×B
Calculating the cross product:
τ=(4a2I^j)×(μ0I2πb^i)
Using the right-hand rule for the cross product:
^j×^i=−^k
Thus, we have:
τ=4a2I⋅μ0I2πb(−^k)=−4μ0I2a22πb^k
This simplifies to:
τ=−2μ0I2a2πb^k
Final Answer
The magnitude of the torque on the loop about the z-axis is:
|τ|=2μ0I2a2πb
The magnetic moment M of a current-carrying loop is given by the formula:
M=I⋅A
where I is the current flowing through the loop and A is the area of the loop.
A=(2a)2=4a2
Thus, the magnetic moment M becomes:
M=I⋅4a2=4a2I
The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
In this case, the distance r from the wire to the center of the square loop is b (since the wire is at point (0,b,0) and the loop is centered at the origin).
B=μ0I2πb
The current in the loop flows in an anti-clockwise direction when viewed from the positive z-axis. Therefore, the direction of the magnetic moment M is in the positive y-direction:
M=4a2I^j
Using the right-hand rule, if the current in the wire flows upwards (in the positive z-direction), the magnetic field at the location of the loop (which is in the xz-plane) will be directed in the positive x-direction:
B=μ0I2πb^i
The torque τ on the loop is given by the cross product of the magnetic moment M and the magnetic field B:
τ=M×B
Calculating the cross product:
τ=(4a2I^j)×(μ0I2πb^i)
Using the right-hand rule for the cross product:
^j×^i=−^k
Thus, we have:
τ=4a2I⋅μ0I2πb(−^k)=−4μ0I2a22πb^k
This simplifies to:
τ=−2μ0I2a2πb^k
The magnitude of the torque on the loop about the z-axis is:
|τ|=2μ0I2a2πb
Topper's Solved these Questions
Similar Questions
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.A square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.
 AThere is no net force on the loopBThe loop will be attracted by the conductor only if the current in the loop flows clockwise.CThe loop will be attracted by the conductor only if the current in the loop flows anticlockwiseDThe loop will always be attracted by the conductor
AThere is no net force on the loopBThe loop will be attracted by the conductor only if the current in the loop flows clockwise.CThe loop will be attracted by the conductor only if the current in the loop flows anticlockwiseDThe loop will always be attracted by the conductor
A square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
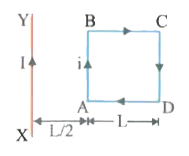
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA square coil ABCD lying in x−y plane with its centre at origin. A long straight wire passing through origin carries a current i=2t in negative z-direction. The induced current in the coil is

View SolutionA square loop ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
View SolutionA square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be

View Solution


