The total number of solution of sin{x}=cos{x} (where {.} denotes the fractional part) in [0,2π] is equal to
Given the equation is sin{x}=cos{x}.
tan{x}=1
tan(π/4)=1<tan1
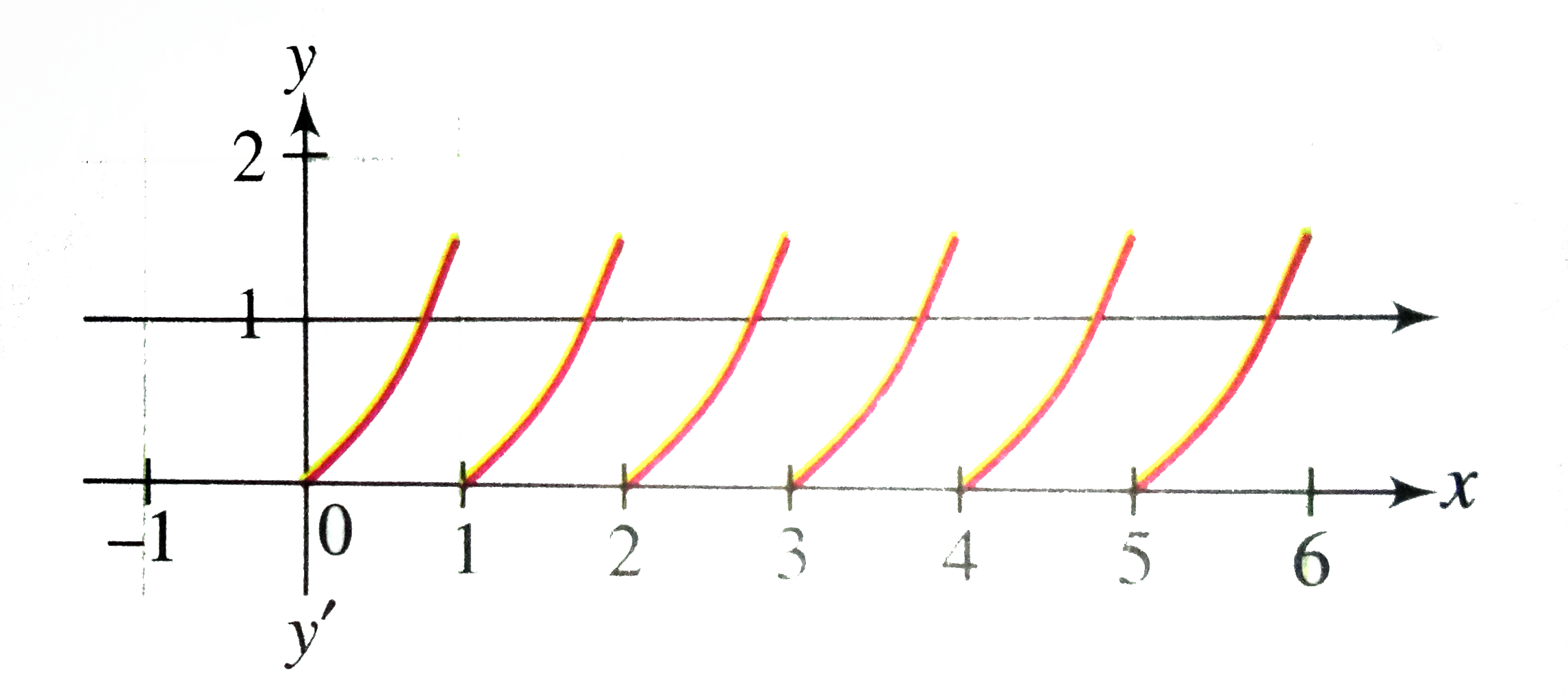
The graphs of y=tan{x} and y = 1 meet exactly six times in [0,2π].
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
Similar Questions
If total number of solution of sin{y}=cos{y}, where {y} denotes the fractional part of y and y∈[0,3π] is c then total number of integral values of b for which the equation x2+bx+c=0 have imaginary roots.
View SolutionThe number of solutions of [sinx]=cosx, where [.] denotes the greatest integer function in [0,3π], is equal to
View Solution
Knowledge Check
- Question 1 - Select One
if f(x)={x2}, where {x} denotes the fractional part of x , then
Af(X) is continuous at x=-2 but not at x=2Bf(x) is continuous at x=2 but not at x=-2Cf(x) is continuous at x=2 and x=-2Df(x) is discontinuous at x=-2 and at x=2 - Question 2 - Select One
The value of ∫40{x}dx (where , {.} denotes fractional part of x) is equal to
A43B53C73DNone of these - Question 3 - Select One
The period of function 2{x}+sinπx+3{x/2}+cosπx (where {x} denotes the fractional part of x) is
A2B1C3DNone of these
Evaluate ∫20{x}dx, where {x} denotes the fractional part of x.
View SolutionThe number of solutions of 4{x}=x+[x] where [.] denotes G.I.F and {.} represents fractional part function is equal to
View SolutionTotal number of solutions of [sin x] + cos x = 0, where [] denotes the greatest integer function, for x e [0, 100π] is (A) 100 (B) 50 (C) 25 (D) 0
View SolutionPeriod of the function f(x)=cos(cosπx)+e{4x}, where {.} denotes the fractional part of x, is
View Solutionlimx→1xsin{x}x−1, where {x} denotes the fractional part of x, is equal to
View Solution

