Find the number of solutions to ${log}_{e} | sin x | = - x^{2} + 2 x$ in $[- \frac{π}{2}, \frac{3 π}{2}]$ .

Text Solution

Verified by Experts

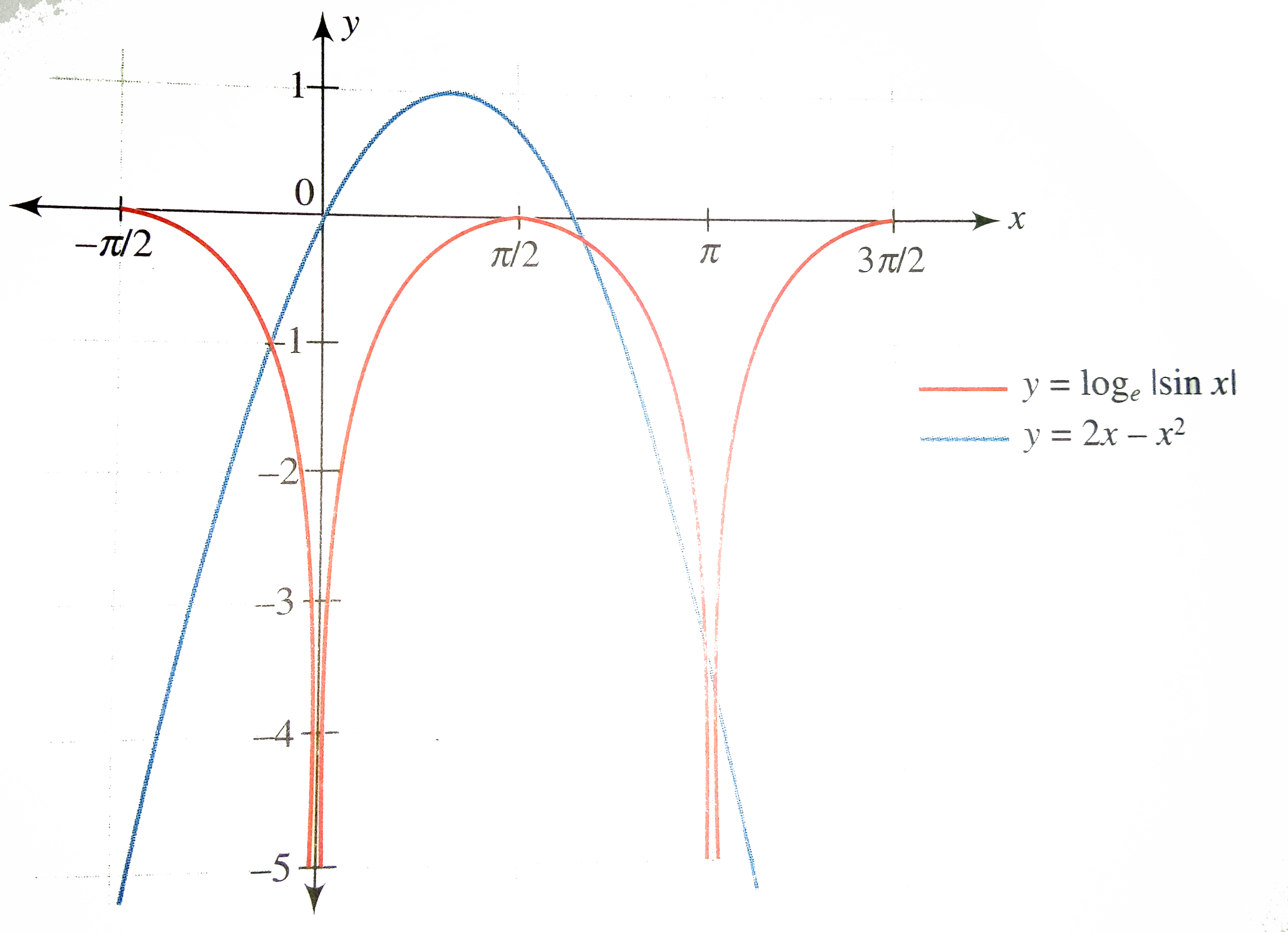
${log}_{e} | sin x | = - x (x - 2)$
Graphs of $y = {log}_{e} | sin x |$ and $y = - x (x - 2)$ meet exactly four times in $[- \frac{π}{2}, \frac{3 π}{2}],$
hence four roots.

|

Updated on:21/07/2023

Class 12 MATHS GRAPHS OF TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34videos
GRAPHS OF ELEMENTARY FUNCTIONS
BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3videos
HIGHT AND DISTANCE

Similar Questions

Knowledge Check

Question 1 - Select One
Number of solutions (s) of in $| sin x | = - x^{2}$ if $x \in [- \frac{π}{2}, \frac{3 π}{2}]$ is/are:
A2
B4
C6
D8
Question 2 - Select One
Find the number of solution of ${log}_{\frac{1}{2}} | sin x | = 2 - {log}_{\frac{1}{2}} | cos x |, x \in [0, 2 π]$
A2
B4
C6
D8

CENGAGE-GRAPHS OF TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile