Consider an equilateral triangle ABC of side 2a in the plane of the paper as shown. The centroid of the triangle is O. Equal charges (Q) are fixed at the vertices A, B and C In what follows consider all motion and situations to be confined the plane of the paper.

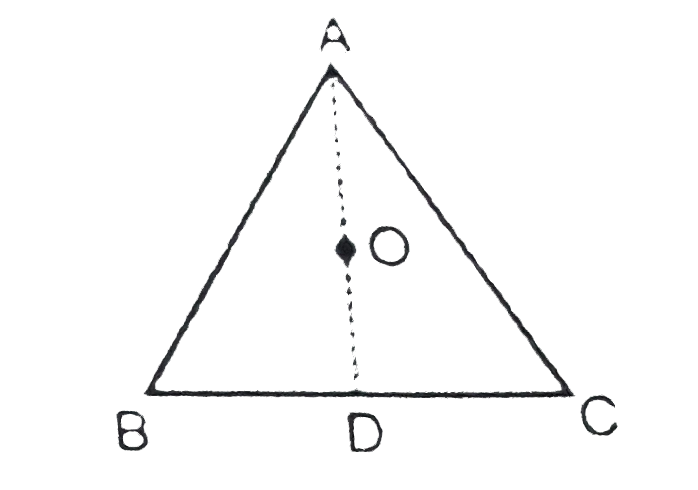
(a) A test charge (q), of same sign as Q is placed on the median AD at a point at a distance $δ$ below O. Obtain the force $(\to F)$ felt by the test charge.
(b) Assuming $δ < < a$ discuss the motion of the test charge when it is released.
(c) Obtain the force $({\to F}_{D})$ on this test charge if it is placed at the point D as shown in the figure.
(d) In the figure below mark the approximate locations of the equilibrium point (s) for this system. Justify your answer.
(e) Is the equilibrium at O stable or unstable if we displace the test in the direction of OP ? The line PQ is parallel to the base BC. Justify your answer.
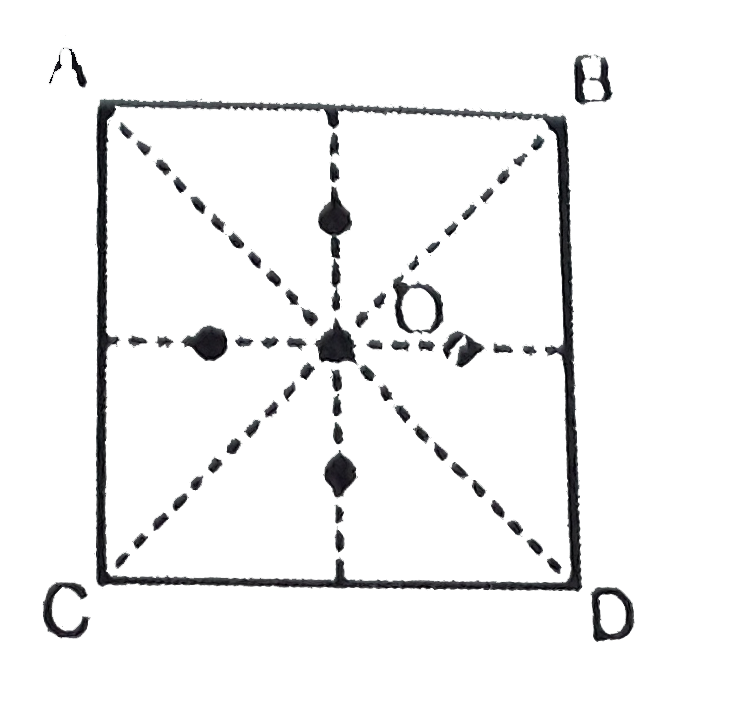
(f) Consider a rectangle ABCD. Equal charges are fixed at the vertices A, B, C and D. O is the centroid. In the figure below mark the approximate locations of all the neutral points of the system for a test charge with same sign as the charges on the vertices. Dotted lines are drawn for the reference.
(g) How many neutral points are possible for a system in which N charges are placed at the N vertices of a regular N sided polygon ?

Text Solution

Verified by Experts

(a) $\to F = \frac{2 K Q q (\frac{a}{\sqrt{3}} - δ)}{{(a^{2} + {(\frac{a}{\sqrt{3}} - δ)}^{2})}^{3 / 2}} - \frac{K Q q}{(\frac{2 a}{\sqrt{3}} + δ)}$ Here $K = 1 / 4 π ε_{0}$ and direction is upward (towards A)
(b) Using binomial approximation, $\to F = K Q q \frac{9 \sqrt{3}}{16} \frac{δ}{a^{3}}$ (upward) which is linear in $δ$ . Hence charge will oscillate simple harmonically about O when relaesed.
(c) ${\to F}_{D} = \frac{K Q q}{3 a^{2}}$ (downward)
(d) For small $δ$ force on the test charge is upwards while for large $δ$ (eq. at D) force is downwards. So there is a neutral point between O and D. By symmetry there will be neutral points on other medians also. In figure x. Below all possible (4) neutral points are shown by.

(e) Let the distance along P be x and O to be at (0, 0). electric potential of a test charge along OP can be written as $V (x) = \frac{K q}{\sqrt{x^{2} + (4 / 3)}} + \frac{K Q}{\sqrt{{(x + 1)}^{2} + (1 / 3)}} + \frac{K Q}{\sqrt{{(x - 1)}^{2} + (1 / 3)}} \approx K Q \sqrt{\frac{3}{4}} (3 + \frac{9}{16} x^{2})$
We can see that $V (x) \propto x^{2}$ , hence it is stable equilibrium.
(f) Equilibrium points are indicated by

(g) $N + 1$

Updated on:21/07/2023

Equal charges $q$ are placed at the vertices $A$ and $B$ of an equilatral triangle $A B C$ of side $a$ . The magnitude of electric field at the point $C$ is
A $\frac{q}{4 π ε_{0} a^{2}}$
B $\frac{\sqrt{2} q}{4 π ε_{0} a^{2}}$
C $\frac{\sqrt{3} q}{4 π ε_{0} a^{2}}$
D $\frac{q}{2 π ε_{0} a^{2}}$
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
A $\frac{q^{2}}{4 \sqrt{2} π ε_{0} l^{2}}$
B $\frac{- q^{2}}{4 π ε_{0} l^{2}}$
C $\frac{q^{2}}{4 π ε_{0} l^{2}}$
Dzero
Consider three charges $q_{1}, q_{2}$ and $q_{3}$ each equal to $q$ , at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?
A $\frac{3 Q q}{4 π ε_{0} l^{2}}$
B $\frac{2 Q q}{4 π ε_{0} l^{2}}$
C $\frac{Q q}{2 π ε_{0} l^{2}}$
Dzero