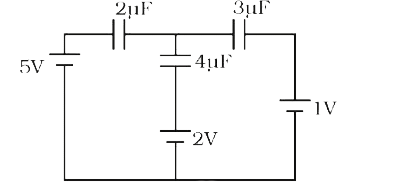
Find the current flowing through the branch AC in the steady state as also the charge on the capacitor C. If the externally applied potentials are now withdrawn, how will the charge on the capacitor vary as a function of time?
(R=1kΩ,C=10μF)
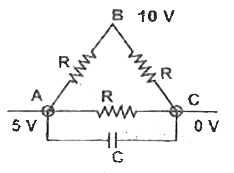
Text Solution
The current through BA=10V−5V1=5mA
Similarly current through AC=5mA,&BC=10mA
steady state charge on C=5V×10μF=50μCIf the potential differences are withdrawn at time t = 0, the charge on the capacitor varies as a function of time as it discharges through the external resistance. The equivalent resistance of the circuit across AC is
2R.R2R+R=23×R=667Ω(≈)
The time constant τ=(2/3R)XXC=6.67msec
The charge across the capacitor decreases exponentiallyq(t)50μCxsxe−t/6.67ms
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
20 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
9 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Illustration
10 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II
15 Videos
Similar Questions
Knowledge Check
The circuit is in a steady state.
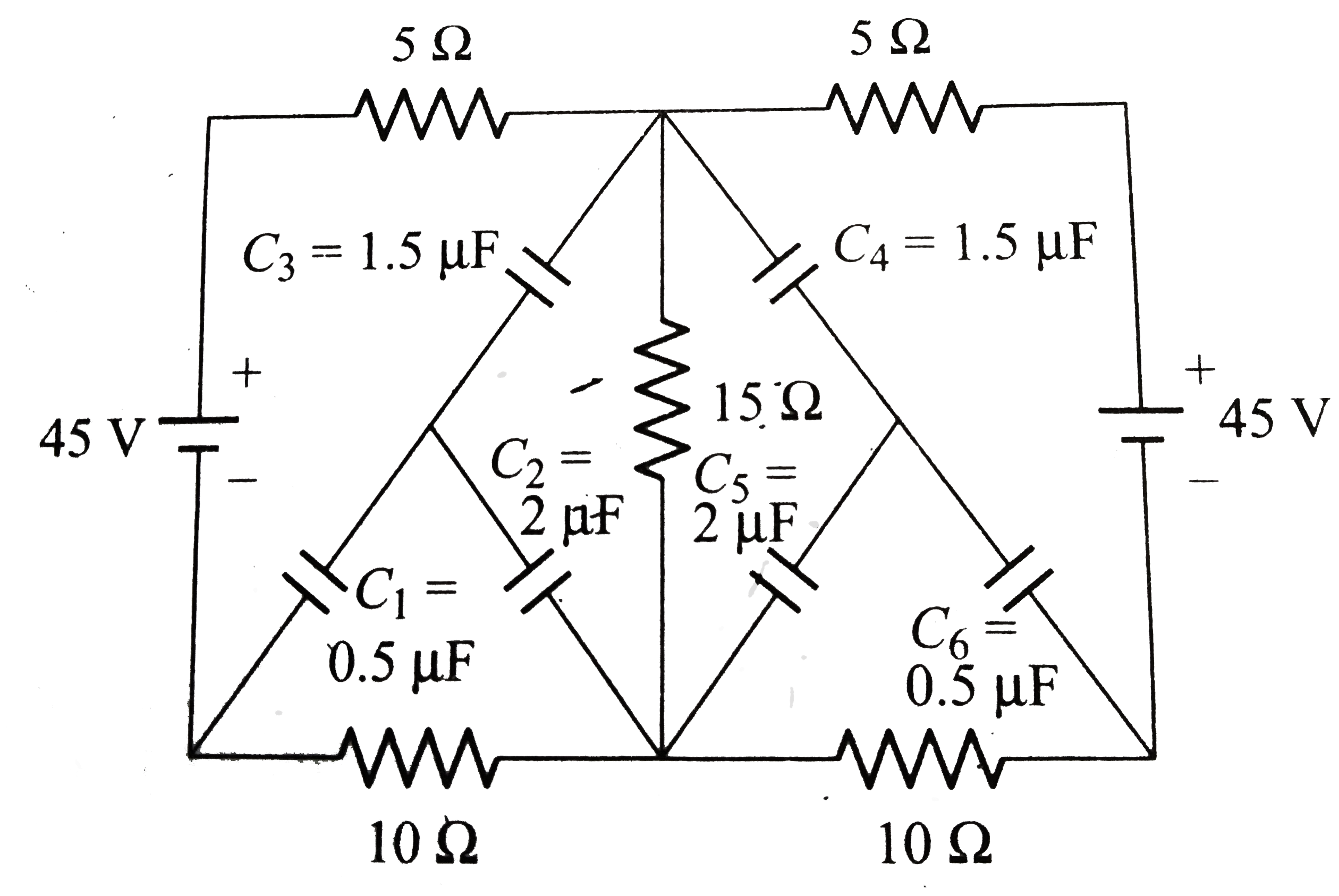
The charge in capacitor C1 isA20μCB30μCC40μCD10μCThe circuit is in a steady state.
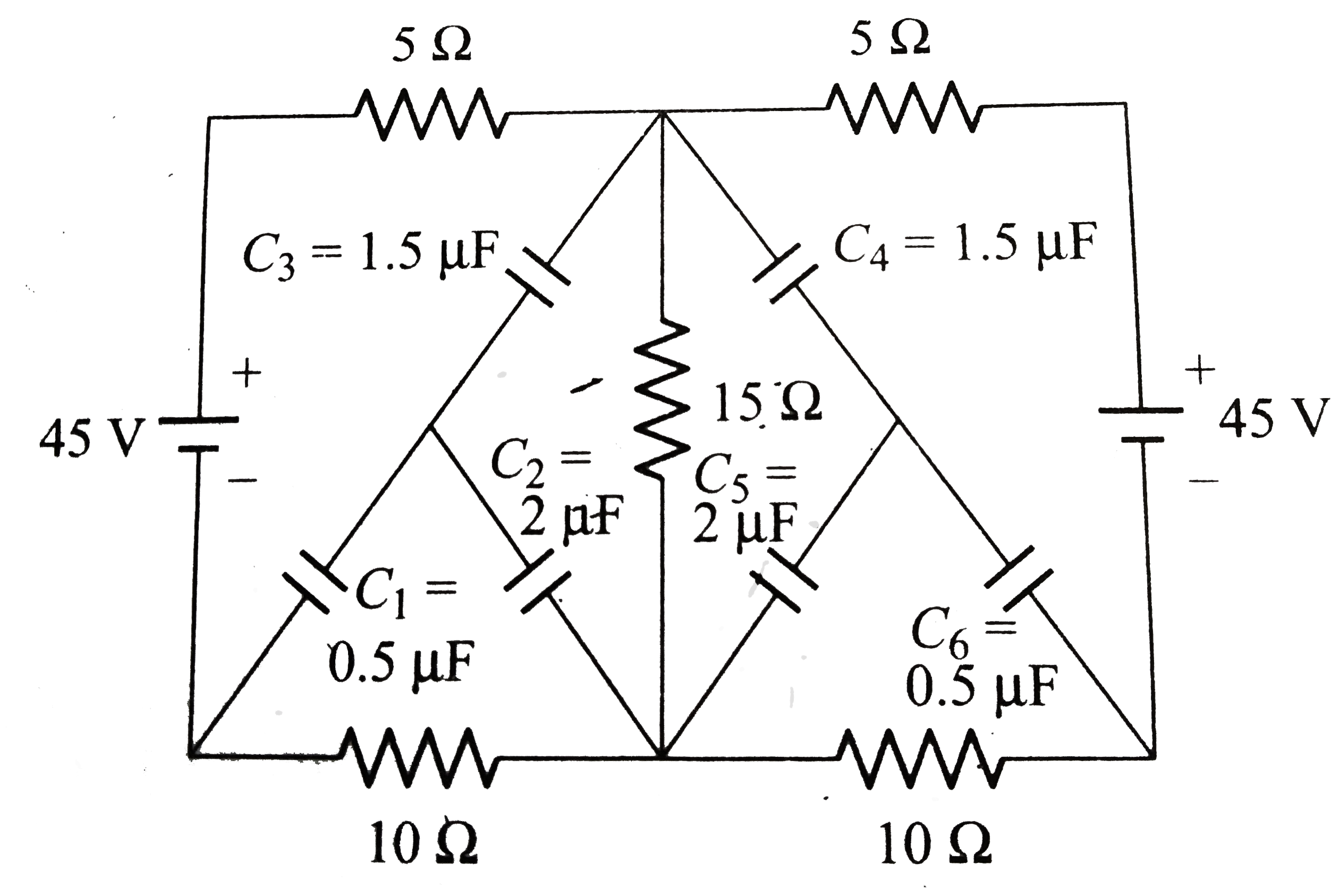
The charge in capacitor C3 isA10μCB30μCC20μCD40μCThe circuit is in a steady state.
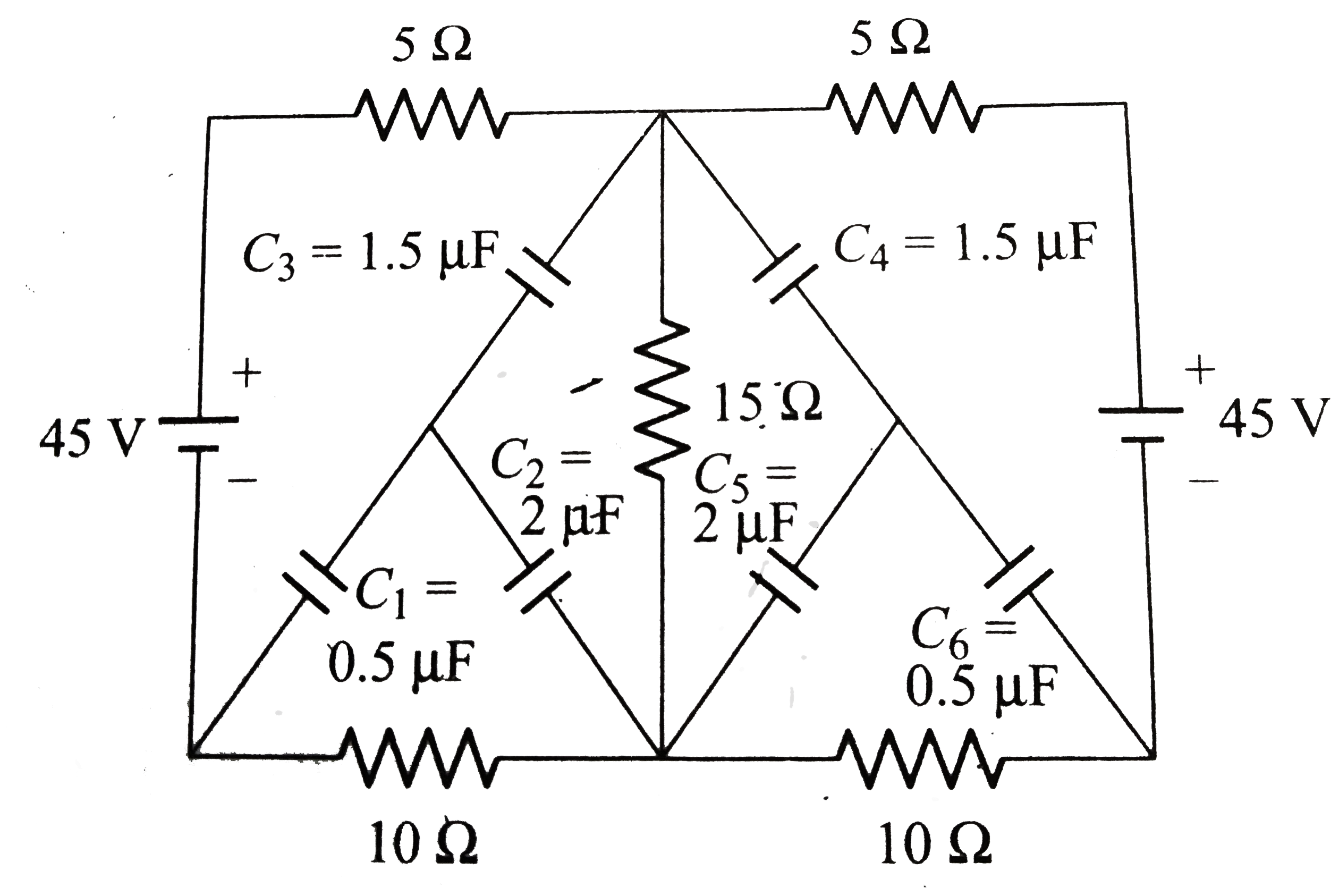
The charge in capacitor C2 isA30μCB10μCC20μCD40μC
Find the current in each branch f the given circuit in steady state. Find the charge on each capacitor.
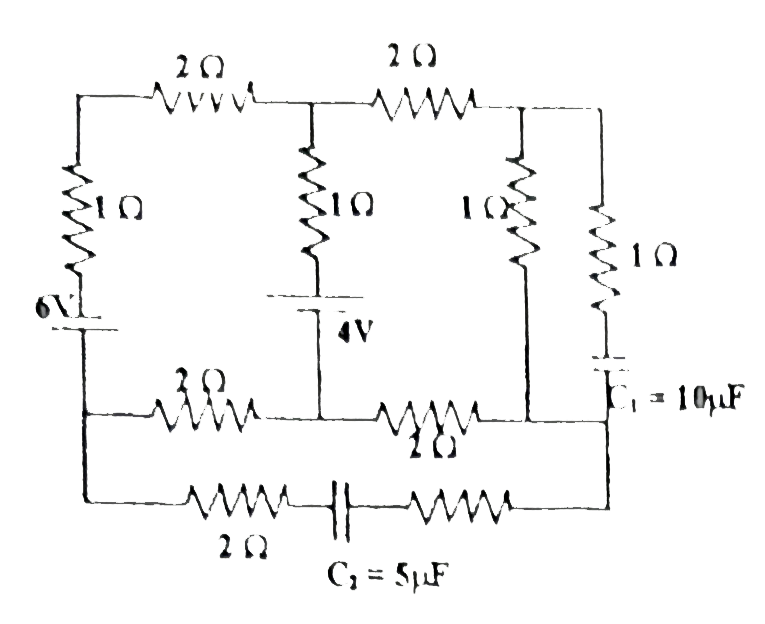
View SolutionFind the current in each branch f the given circuit in steady state. Find the charge on each capacitor.

View SolutionThe circuit is in a steady state.

The charge in capacitor C1 is
View SolutionThe circuit is in a steady state.

The charge in capacitor C3 is
View SolutionThe circuit is in a steady state.

The charge in capacitor C2 is
View Solution