Consider a Wheatstone bridge with resistance and capacitance connected as shown Find the condition on the resistance and the capacitance such that the bridge remains balanced at all times.
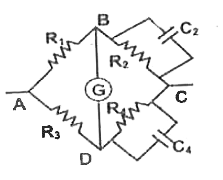
Suppose that the bridge is balanced i.e. VAB=VAD and VBC=VDCLet the current and the charges on the capacitors in the circuit as shown then
I1R1=I3R3l.s(i)
(q2C2=(q4C4ldots(ii)
Consider the charging of the part of the circuit shown alongside. Let qz be the charge on C2 and i1 be the current in the circuit. Then
I1R1+q2C2=ε...(iii)
dq2dt+q2R2C−(2)=i1...(iv)
Substituting (iv) in (ill) and simplifying
dq2dt+q2ReqC2=εR1where1Req=1R1+1R2
thereforeq2=εR4C4R1[1−e1REqC4]=εR2C2R1+R2[1−e−1/ReqC2]
Similarly, for the other circuit, we haveq4=εR4C4R3+R4[1−e1ReqC4],where1Req=1R3+1R4
NOW,q2C2=(q4C−(4)),which leads to
R2R1+R2=R4R3+R4and1ReqC2=1ReqC2OrR1R2=R3R4andR1C2=R3C4
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
20 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
9 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Illustration
10 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II
15 Videos
Similar Questions
Knowledge Check
In a Wheatstone bridge resistance connected the bridge is balanced , when the resistance are in the ratio
 APQ=RSBQP=SRCPQ=RSDPQ=SR
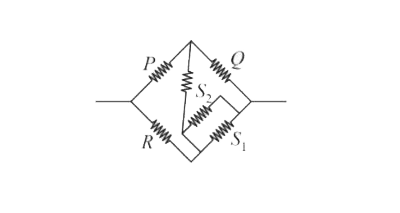
APQ=RSBQP=SRCPQ=RSDPQ=SRIn a Wheatstone's bridge, three resistances P,Q and R connected in the three arms and the fourth arm is formed by two resistances S1andS2 connected in parallel. The condition for the bridge to be balanced will be
APQ=2RS1+S2BPQ=R(S1+S2)S1S2CPQ=R(S1+S2)2S1S2DPQ=RS1+S−2In a wheatstone bridge resistance of each of the four sides is 10Ω. If the resistance of the galvanometer is also 10Ω , then effective resistance of the bridge will be
A10ΩB5ΩC20ΩD40Ω
In a Wheatstone's bridge, three resistances P,Q and R connected in the three arms and the fourth arm is formed by two resistances S1andS2 connected in parallel. The condition for the bridge to be balanced will be
View SolutionIn a Wheatstone's bridge, three resistances P,Q and R connected in the three arms and the fourth arm is formed by two resistances S1andS2 connected in parallel. The condition for the bridge to be balanced will be
View SolutionDerive the condition of balance for Wheatstone bridge.
View SolutionIn a wheatstone bridge resistance of each of the four sides is 10Ω. If the resistance of the galvanometer is also 10Ω , then effective resistance of the bridge will be
View SolutionIn a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)
View Solution
