If (x,y) is a variable point on the line y=2x lying between the lines 2(x+1)+y=0 and x+3(y−1)=0 , then x∈(−12,67) (b) x∈(−12,37) y∈(−1,37) (d) y∈(−1,67)
x∈(−1/2,6/7)
x∈(−1/2,3/7)
y∈(−1,3/7)
y∈(−1,6/7)
The correct Answer is:B, D
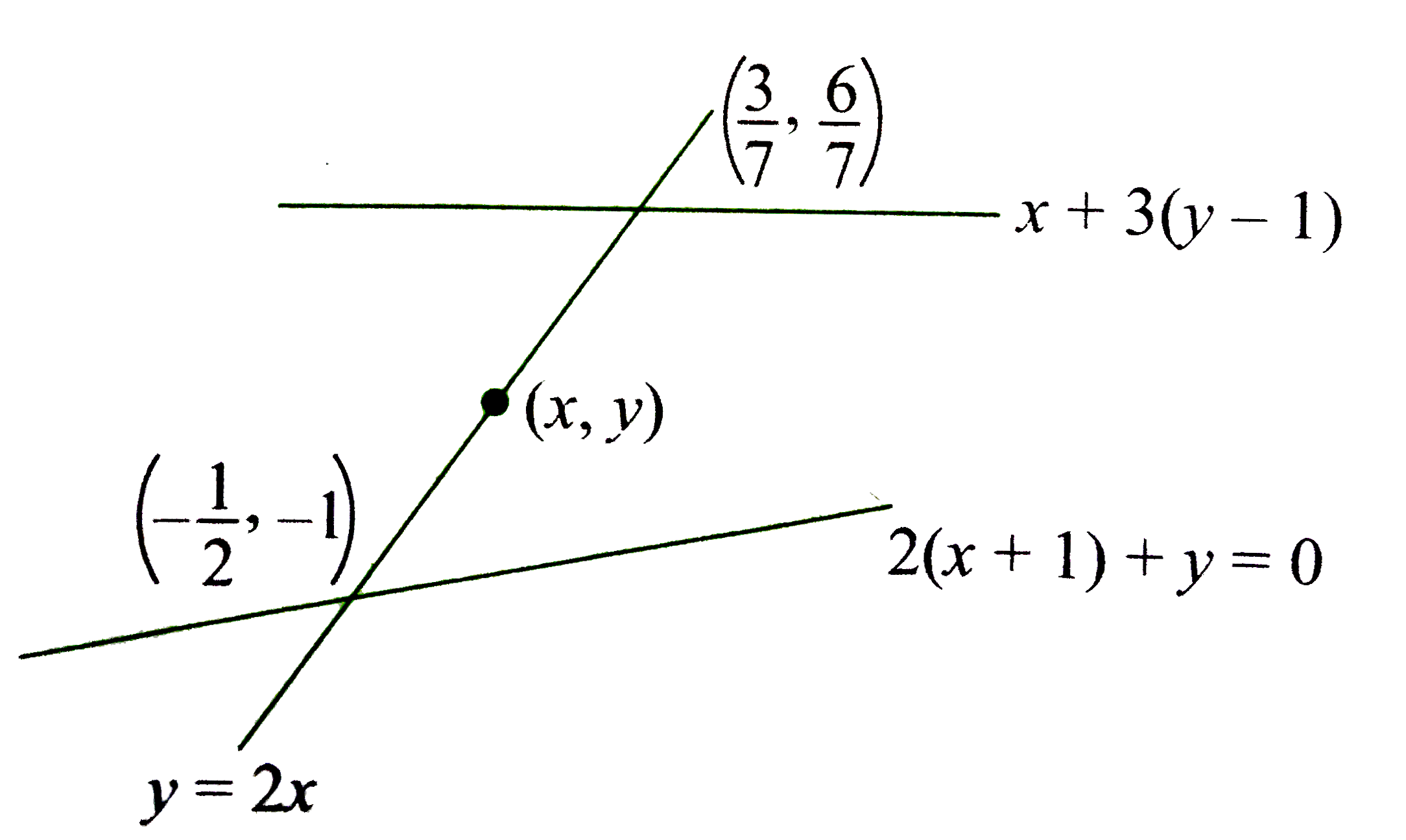
Solving y=2x, 2(x+1) + y = 0, we get x = -1/2, y=-1. Solving y=2x, x+3(y-1)=0, we get x=3/7, y=6/7.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)8videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Single)82videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
If (x,y) is a variable point on the line y=2x lying between the lines 2(x+1)+y=0 and x+3(y−1)=0 , then (a) x∈(−12,67) (b) x∈(−12,37) (c) y∈(−1,37) (d) y∈(−1,67)
View SolutionWhat are the coordinates of the point of intersection of the lines x+3y=7 and 2x+y=−1?
View SolutionThe equation of the bisector of the obtuse angle between the lines x−y+2=0, 7x+y+1=0 is
View SolutionThe orthocentre of the triangle formed by the lines x−7y+6=0,2x−5y−6=0and7x+y−8=0 is
View SolutionFind the angle between the lines x+12=y3=z−36 and the planes 3x+y+z=7.
View SolutionFind the angle between the lines
5−x3=y+3−4,z=7 and x1=1−y2=z−62View SolutionThe angle between the line joining the points (1, -2) , (3, 2) and the line x+2y-7=0 is
View SolutionFind the angle between the line x1=y2=z3 and x+12=y−3−7=z+24
View SolutionFind the angle between the line joining the points (1,-2), (3,2) and the line x+2y−7=0
View SolutionThe angle between the line joining the points (1,-2) , (3,2) and the line x+2y -7 =0 is
View Solution

