Question

Let $P(\sin \theta ,\cos \theta )$ $(0\le \theta \le 2\pi )$ be a point and let OAB be a triangle with vertices $(0,0),(\sqrt{\frac{3}{2}},0)\text{and}(0,\sqrt{\frac{3}{2}})$ Find $\theta$ if P lies inside $△OAB$

Options

A. `0 lt 0 lt pi//12`
B. `5pi//2 lt theta lt pi//2`
C. `0 lt theta lt 5pi//2`
D. `5pi//2 lt theta lt pi`

Answer

A::B

Explanation

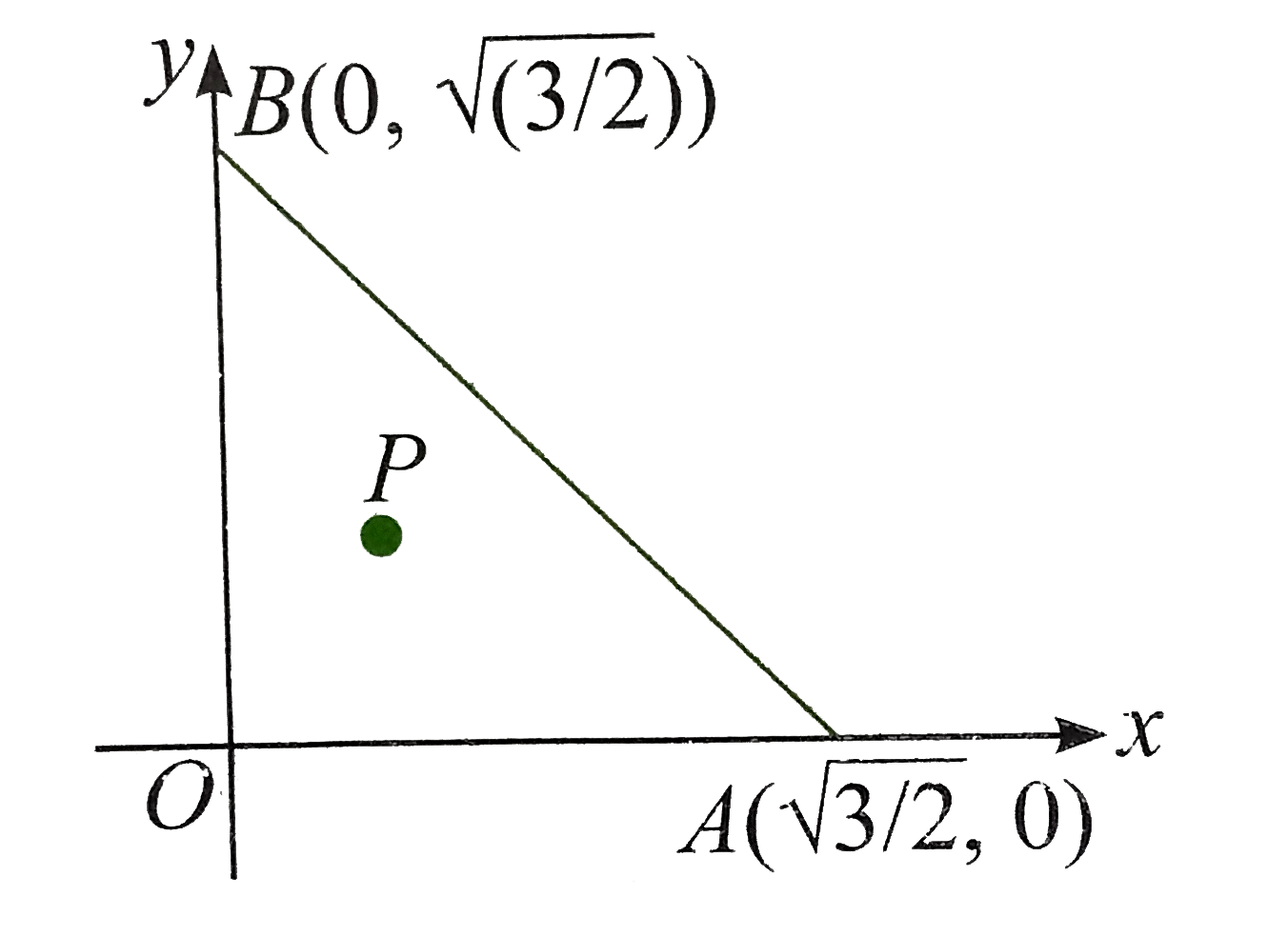
The equations of lines along OA, OB and AB are y=0, x=0, and x+y `=sqrt(3//2)`, respectively.
Now, P and B will lie on the same side of y=0 if `"cos" theta gt 0`. Similarly, P and A will lie on the same side of x=0 if `"sin " theta gt 0`, and P and O will lie on the same side of `x+y = sqrt(3//2) " if sin " theta + "cos" theta lt sqrt(3//2)`. Hence, P will lie inside `Delta ABC "if sin" theta gt 0, "cos " theta gt 0, " and sin " theta + "cos " theta lt sqrt(3//2),` Now,
`"sin "theta + "cos "theta lt sqrt((3)/(2))`
`"or sin"(theta + (pi)/(4)) lt sqrt((3)/(4))`
Since `"sin "theta gt 0 " and cos "theta gt 0, 0 lt theta lt pi//12 " or " 5pi//12 lt theta lt pi//2.`