Doubtnut Promotions Sticky

Draw the graph of y=cos−1(1+x21+x2)

Text Solution
Verified by Experts

We have y=f(x)=cos2(1+x21+x2)
Let x=tanθ,θ∈(−π/2,π/2)
⇒ θ=tan−1x
Now cos−1(1−x21+x2)=cos−1(1−tan2θ1+tan2θ)
=cos−1(cos2θ)
=cos−1(cos2θ), where α∈(−π,π)
Now consider the graph of y=cos−1(cosα), where α∈(−π,π)
ocr_image
From the graph.
cos−1(1−x21+x2)=cos−1(cosα)
={−α−π<α<0α0≤α<π
={−2tan−1x−π<2tan−1x<02tan−1x0≤2tan−1x<π
={−2tan−1x−π<2tan−1x<02tan−1x0≤2tan−1x<π/2
={−2tan−1xx<02tan−1xx≥0
f'(x)=⎧⎨⎩−21+x2x<021+x2x>0
So f(x) is non-differentiable at x = 0
limx→∞(−2tan−1x)=π,f(0)=2tan−1(0)=0
Thus, cos−1(1−x21+x2) decreases form π to 0 as increases from−∞ to 0.
limx→∞(2tan−1x)=π
Thus, cos−1(1−x21+x2) increases form 0 to π as x increses from 0 to∞.
From this information, we can draw the graph of y=cos−1(1−x21+x2) as shown in the following figure.
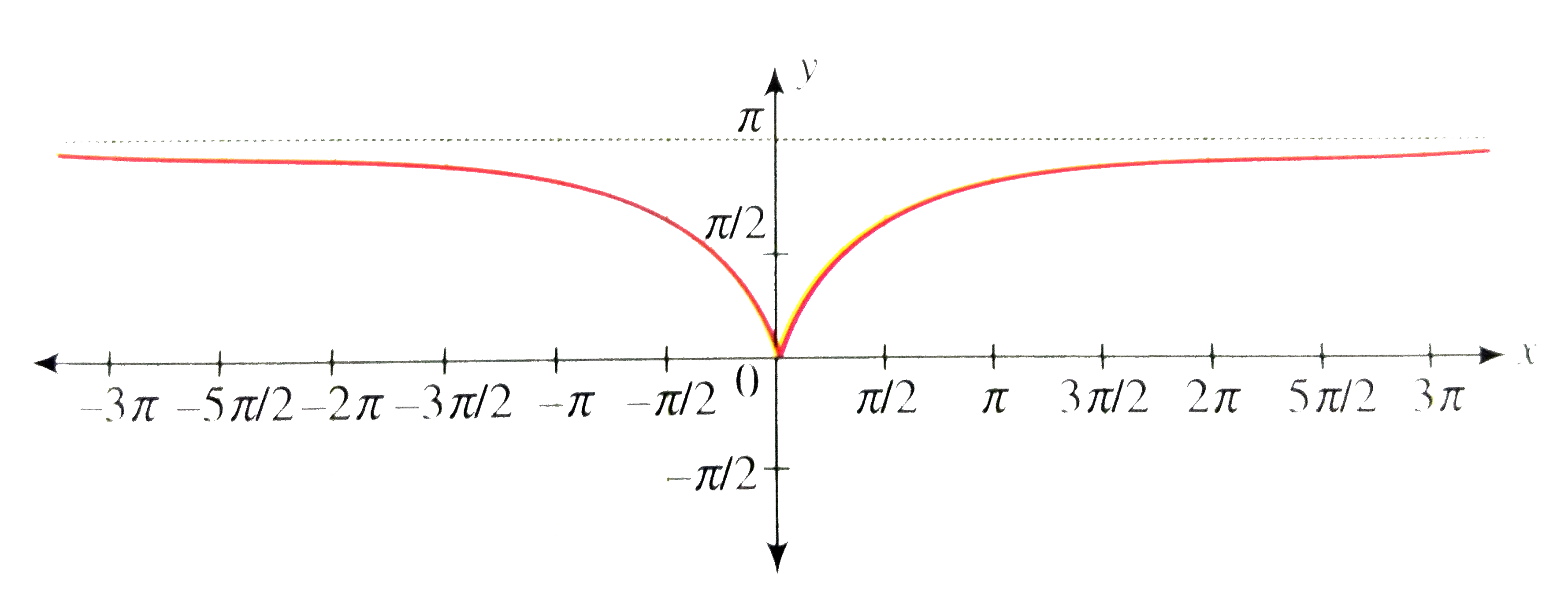
ocr_image

Doubtnut Promotions Banner
|