In a conservative field, U=sinx+cosx. Select the connect
x=π4 is position of stable equilibrium
x=3π4 equilibrium
x=3π4 is position of stable equilibrium
x=π4 equilibrium
For stable equilibrium
dUdx=0 and d2Udx2>0
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The potential energy of a particle of mass 1 kg in a conservative field is given as U=(3x2y2+6x) J, where x and y are measured in meter. Initially particle is at (1,1) & at rest then:
AInitial acceleration of particle is 6√5ms2BWork done to slowly bring the particle to origin is 9 JCWork done to slowly bring the particle to origin is −9 JDIf particle is left free it moves in straight line - Question 2 - Select One or More
The potential energy U of a body of unit mass moving in one dimensional conservative force field is given by U=x2−4x+3. All units are is SI. For this situation mark out the correct statement (s).
AThe body will perform simple harmonic motion about x=2 units.BThe body will perform oscillatory motion but not simple harmonic motion.CThe body will perform simple harmonic motion with time period √2πs.DIf speed of the body at equilibrium position is 4ms, then the amplitude of oscillation would be 2√2m - Question 3 - Select One
A particle in a certain conservative force field has a potential energy given by U=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk
Recall that sinx+cosx=u (say)
and sinxcosx=v (say) are connected by
(sinx+cosx)2=sin2x+cos2x+2sincosx
⇒u2=1+2v
⇒v=u2−12
It follows that any rational integral function of sinx+cosx, and sinxcosx i.e., R(sinx+cosx,sinxcosx), or in our notation R(u,v) can be transformed to R(u,u2−12). Thus, to solve an equation of the form R(u,v)=0, we form a polynomial equation in u and than look for solutions.
The solution set of
sinx+cosx−2√2sinxcosx=0 is completely described byView SolutionRecall that sinx+cosx=u (say)
and sinxcosx=v (say) are connected by
(sinx+cosx)2=sin2x+cos2x+2sincosx
⇒u2=1+2v
⇒v=u2−12
It follows that any rational integral function of sinx+cosx, and sinxcosx i.e., R(sinx+cosx,sinxcosx), or in our notation R(u,v) can be transformed to R(u,u2−12). Thus, to solve an equation of the form R(u,v)=0, we form a polynomial equation in u and than look for solutions.
The solution of
sinx+cosx−2√2=0 is completely described byView SolutionRecall that sinx+cosx=u (say)
and sinxcosx=v (say) are connected by
(sinx+cosx)2=sin2x+cos2x+2sincosx
⇒u2=1+2v
⇒v=u2−12
It follows that any rational integral function of sinx+cosx, and sinxcosx i.e., R(sinx+cosx,sinxcosx), or in our notation R(u,v) can be transformed to R(u,u2−12). Thus, to solve an equation of the form R(u,v)=0, we form a polynomial equation in u and than look for solutions.
The number of solutions of the equation sinθ+cosθ=1+sinθcosθ in the interval [0,4π] isView SolutionFigure given below shows the plot of the conservative force F, in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is :
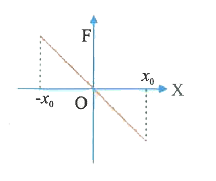 View Solution
View SolutionFigure shows a plot of the conservative force F in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is
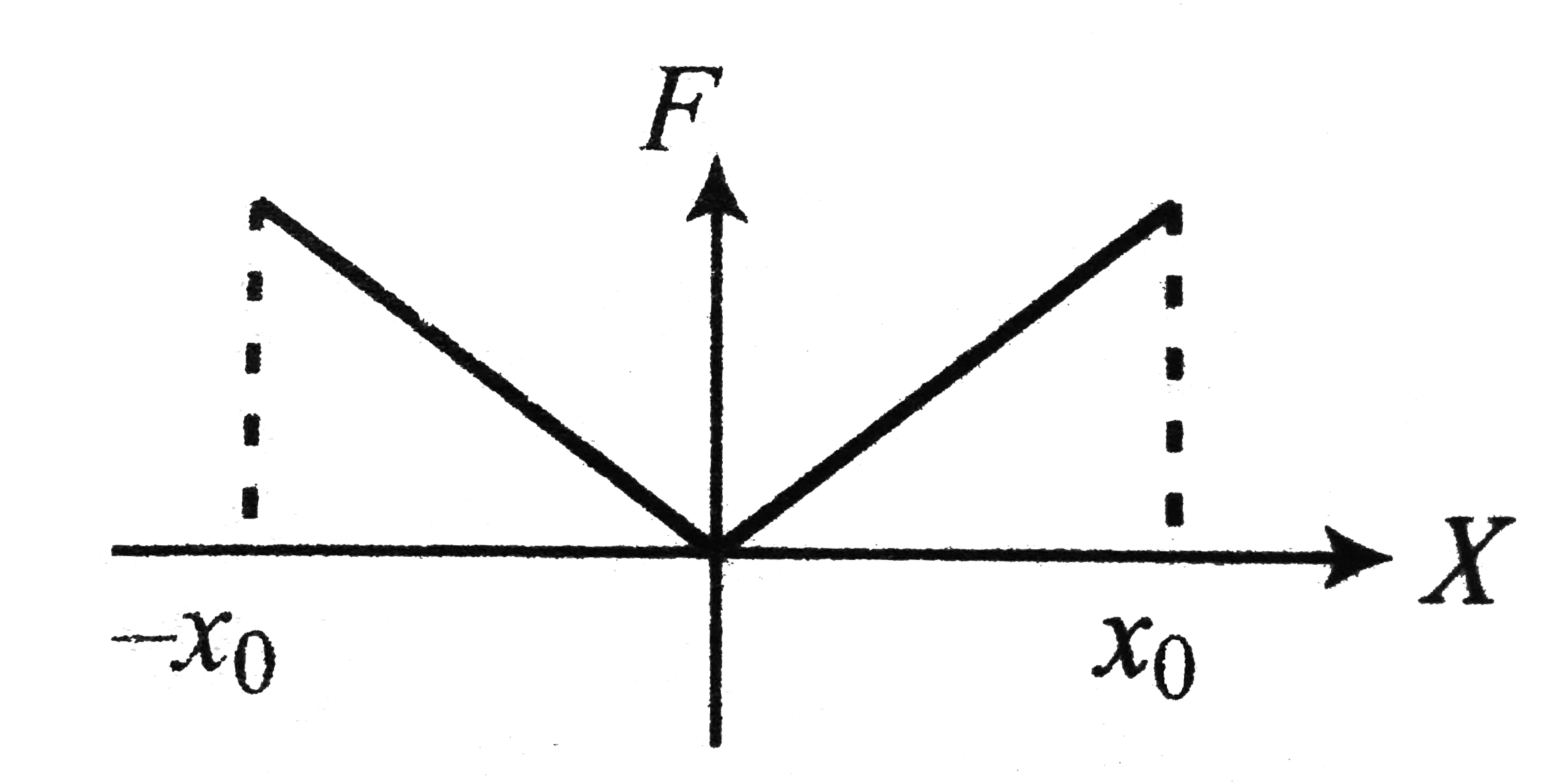 View Solution
View Solution

