The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio ofSolution in Telugu
1:1
1:2
2:1
4:1
The correct Answer is:C
Step by step video, text & image solution for The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 2 (RIGIDITY MODULUS AND BULK MODULUS )16videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 2 (STRAIN ENERGY )16videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE IB (ASSERTION (A) AND REASON ( R) TYPE QUESTIONS (BULK MODULUS; RIGIDITY MODULUS; STRAIN ENERGY; POISSION.S RATIO))12videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-343videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise84videos
MOTION IN A PLANE
Similar Questions
A 2 cm cube o some substance has its upper face displaced by 0.15cm due to a tangential force of 0.3 N Calculate the rigidity modulus of the substance.
04:08View SolutionA wire can be broken by 400 kg.wt. The load required to break the wire of double the thickness of the same material will be
02:32View Solution(A) : Bulk modulus of elasticity (B) represents incompressibility of the material.
(R) : Bulk modulus of elasticity is proportional to change in pressure.04:00View SolutionA U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5cm of spirit in the other. What is the specific gravity of spirit.
04:03View SolutionA person runs along a circular path of radius 5m. Find the magnitude of the displacement if he runs all the way around the circle ?
02:46View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
04:33View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View Solutionस्टील का यंग प्रत्यास्थता गुणांक, पीतल से दोगुना है | एक ही लम्बाई तथा एक ही अनुप्रस्थ काट के दो तारों, एक स्टील का तथा एक पीतल का, को एक ही छत से लटकाया जाता है | यदि, भार लटकाने पर, दोनों तारों के निचले सिरे एक ही तल पर हैं तो स्टील तथा पीतल के तारों से लटकाये भारों का अनुपात होना चाहिये :
03:34View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
02:32View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
05:34View SolutionIf the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
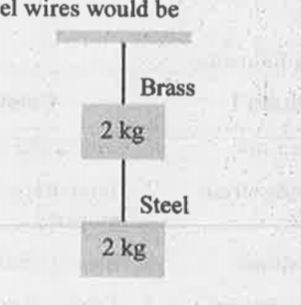 02:25View Solution
02:25View SolutionThe Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
03:08View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
02:06View SolutionThe Young's modulus of steel is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of:
04:00View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
04:00View Solution

