A rocket with an initial mass m0 is going up with a constant acceleration a by exhausting gases with a velocity v relative to the rocket motion, then the mass of the rocket at any instant of time is (assume that no other forces act on it)
m=m0e−atv
m=m0e−2atv
m=m0e−at2v
m=m0e−a2t2v2
The correct Answer is:A
For a rocket,
mdvdt=Fext+vdmdt
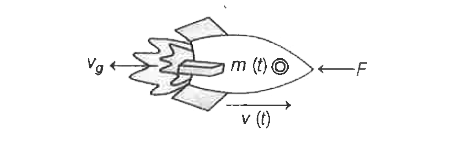
Without any external force (Fext=0),
mdvdt=vdmdt⇒∫dvv=∫dmm
⇒logv=logm+C
When, v=0,m=m0
∴C=−logm0
So, we have
Δvv=logmm0⋅dtorm=m0e−at/v
Topper's Solved these Questions
Similar Questions
A double stage rocket has an initial mass Mi, gas is exhausted front he rocket at a constant rate of dm/dt and with an exhaust velocity u relative to the rocket. When the mass of the rocket reaches the value μ, the first stage of mass m of
Which fuel is exhausted is disengaged from the rocket and then the rocket continues to the second stage at teh same rate and exhaust velocity as int eh first stage, until it reaches a mass Mf
(a). Calculate the rocket velocity at the end of the first stage, given that it is started at rest.
(b). Calculat ethe rocket velocity at the end of the second stage. ltbr> (c). What is the final velocity of a one stage rocket of the same initial Mi mass and the same amount of fuel ? it is greater or less than final velocity of the double stage rocket?
View SolutionA rocket with initial mass M is launched by emitting, gas wil velocity v0 (relative to the rocket body) downwards. The mass of the gas emitted per seconds is k. (k is constant and obeys kv0<Mg). Find time when rocket start to lift.
View Solution
Knowledge Check
Suppose a rocket with an intial mass M0 eject a mass Δm in the form of gases in time Δt, then the mass of the rocket after time t is :-
AM0−ΔmΔt.tBM0−ΔmΔtCM0−ΔmΔtDM0
Find the law according to which the mass of the rocket varies with time, when the rocket moves with a constant acceleration w, the external forces are absent, the gas escapes with a constant velocity u relative to the rocket, and its mass at the initial moment equals m0.
View SolutionFind the mass of the rocket as a function of time, if it moves with a constant acceleration a, in absence of external forces. The gas escapes with a constant velocity u relative to the rocket and its mass initially was m0.
View SolutionFind the mass of the rocket as a function of time, if it moves with a constant acceleration a, in absence of external forces. The gas escapes with a constant velocity u relative to the rocket and its mass initially was m0.
View SolutionA rocket moves in the absence of external forces by ejecting a steady jet with velocity u constant relative to the rocket. Find the velocity v of the rocket at the moment when its mass is equal to m, if at the initial moment it possessed the mass m0 and its velocity was equal to zero. Make use of the formula given in the foregoing problem.
View SolutionSuppose a rocket with an intial mass M0 eject a mass Δm in the form of gases in time Δt, then the mass of the rocket after time t is :-
View SolutionA relativistic rocket emits a gas jet with non-relativistic velocity u constant relative to the rocket. Find how the velocity v of the rocket depends on its rest mass m if the initial rest mass of the rocket equals to m0.
View SolutionA rocket of initial mass 6000kg ejects mass at a constant rate of 16kg/s with constant relative speed of 11m/s What is the acceleration of the rocket one mnute after blast ?
View Solution
