For the arrangement shown on the figure , the string is tightly wrapped over the pilley . Find the acceleration of each block when released from rest . The string is not slipping over the pulley .

The free body diagramms of the pulley and the blocks are shown in the figure
Note that tensions on two sides of the pulley are different .
Applying Newton.s second law on the pulley ,
we get τ=T1R−T2R=(T1−T2)R
Since τ=Iα=(MR2a)α

Therefore (T1−T2)R=(MR22)α
or T1−T2=(MR2)α ....(i)
Alpplying Newton.s Law on the blocks , we get
T2−m2g=m2a2 ...(ii)
m1g−T1=m1a1 ....(iii)
Since the string is tightly wrapped over the pulley , therefore
a1=a2=αR=a.....(iv)
Solving equations (i),(ii),,(iii)and (iv) , we obtain
a=⎡⎣m1−m2m1+m2+M2⎤⎦g
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Consider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View Solution
Knowledge Check
In the arrangement shown in figure, the string are light and inextensible. The surface over which blocks are placed is smooth. Find
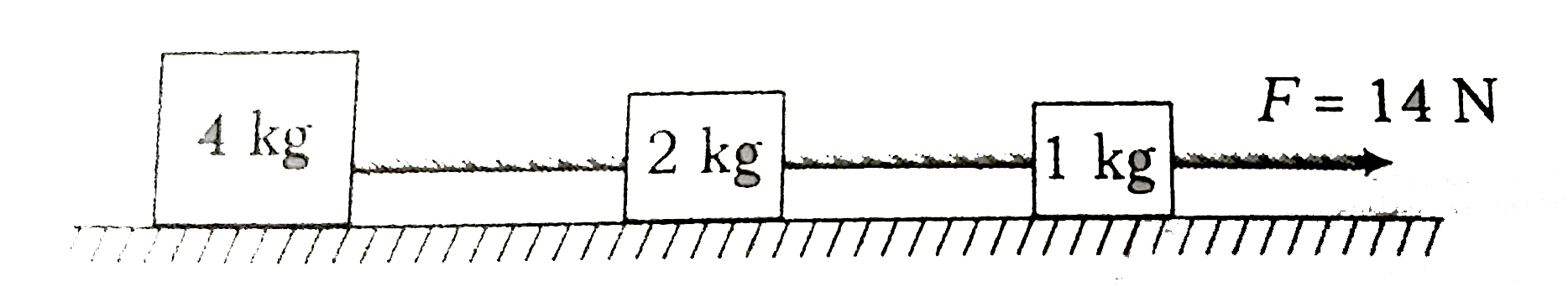
(a) the accelrations of the block
(b) the tension in each string.Aa=8m/s2 , T1=12N, T2=12NBa=4m/s2 , T1=12N, T2=8NCa=4m/s2 , T1=24N, T2=8NDa=4m/s2 , T1=24N, T2=24NIn the arrangement shown in fig. The strings are light and inextensible. The surface over which blocks are placed is smooth. Find:

(a) the acceleration of each block.
(b) the tension in each string.Aa=4ms−2 b=16N , 24NBa=6ms−2 b=12N , 24NCa=−4ms−2 b=16N , 12NDa=−5ms−2 b=26N , 24N
In the arrangement shown in figure. The strings are light and inextensible. The surface over which block are placed is smooth.Find
(a) the acceleration of each block,
(b) the tension in each string.

View SolutionIn the arrangement shown in figure. The strings are light and inextensible. The surface over which block are placed is smooth.Find
(a) the acceleration of each block,
(b) the tension in each string.

View SolutionIn the arrangement shown in figure, the string are light and intextensible. The surface over which blocks are placed is smooth. Find
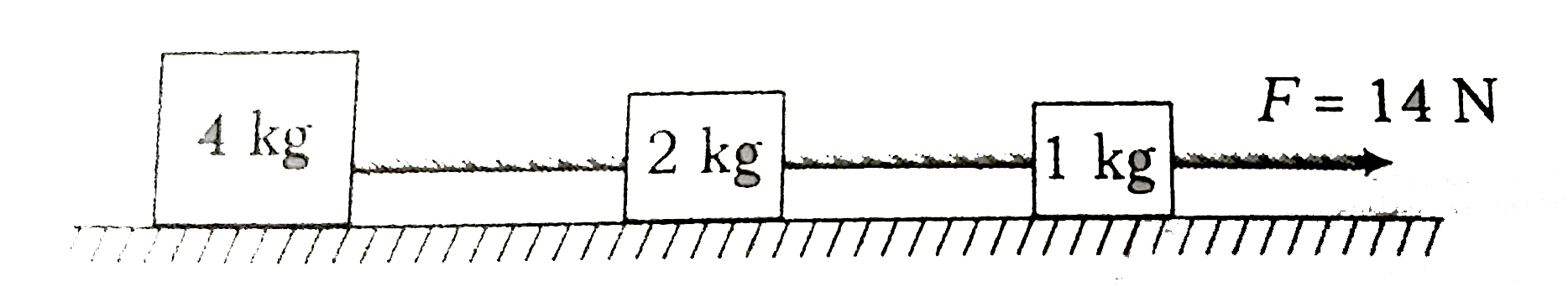
(a) the accelrations of the block
(b) the tension in each string.
View SolutionIn the system shown in figure, the block A is released from rest. Find
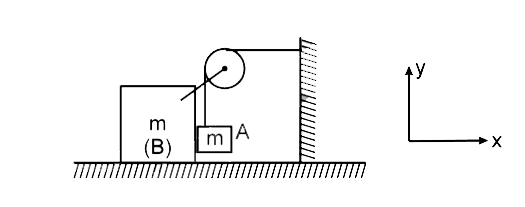
Tension in the string.
View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
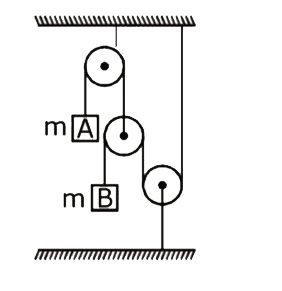
View SolutionIn the arrangement shown in fig. The strings are light and inextensible. The surface over which blocks are placed is smooth. Find:

(a) the acceleration of each block.
(b) the tension in each string.
View Solution
