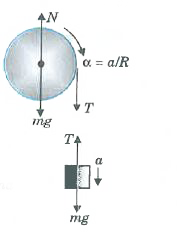
A mas m hangs with help of a string wraped around a pulley on a frictionless bearling. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is:
g
23g
g3
32g
The correct Answer is:B
T is the tension in string Using Newton.s law of motion, we have,
mg−T=ma …….(i)
Torque acting on the pulley is
TR=Iα=mR22α
[∴a=Rα]
T=mRα2=ma2
From equation (i) mg−ma2=ma
3ma2=mg
a=2g3
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
67 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
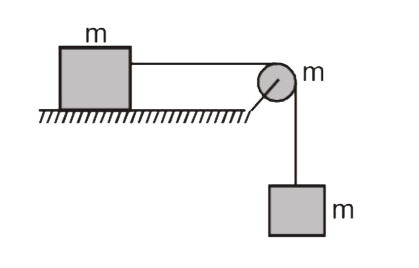
Figure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
View Solution
Knowledge Check
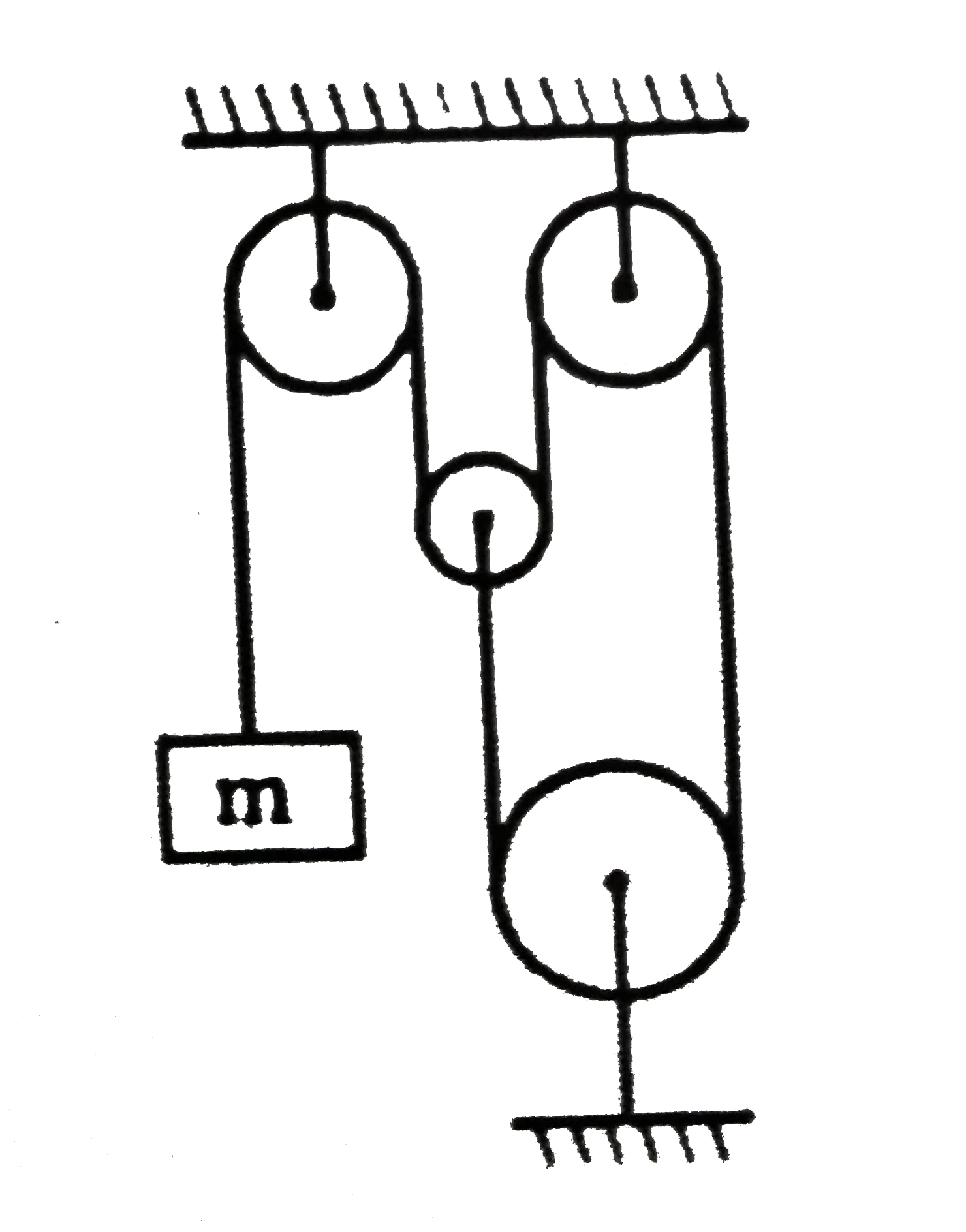
If the string & all the pulleys are ideal, acceleration of mass m is :-
 Ag2B0CgDdependent on m
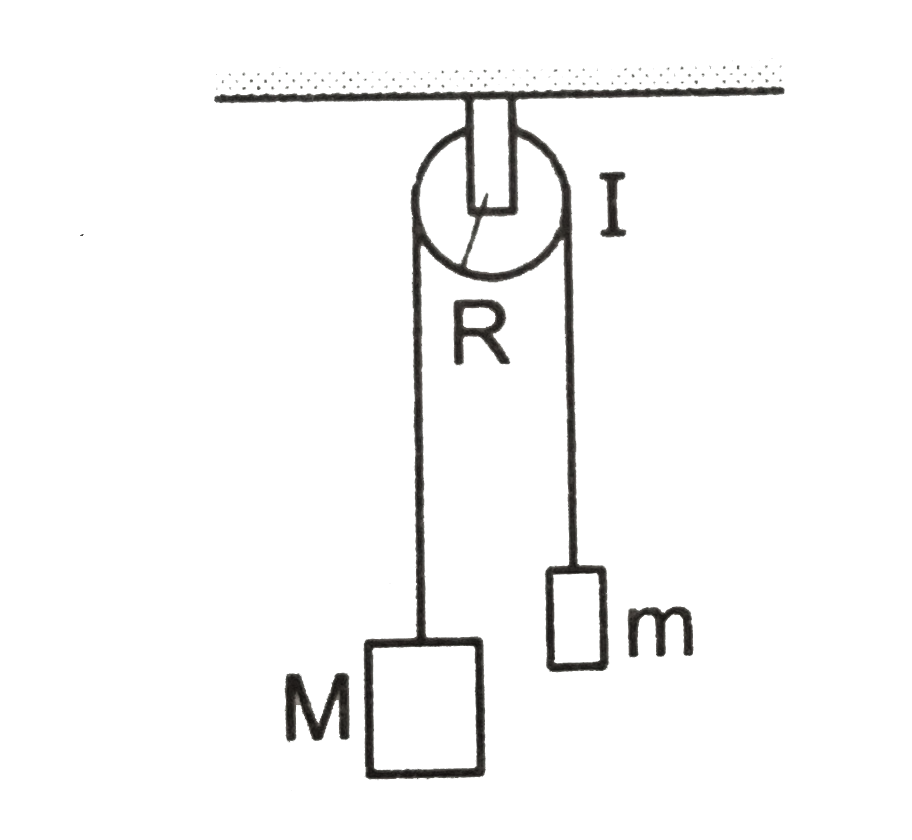
Ag2B0CgDdependent on mA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+M
String is wrapped over a pulley and free end is fixed to the ceiling as shown in figure. Mass of the pulley is m and its radius is R. Assume that pulley is identical to dise. Calculate acceleration of pulley as it is allowed to fall by unwinding the string. Assume that string does not slip over the pulley.

View SolutionFigure shows two blocks of masses m and M connected bky a string pasing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotte about this axis. Find the accelerationof the mass M asuming that the string does not slip on the pulley.
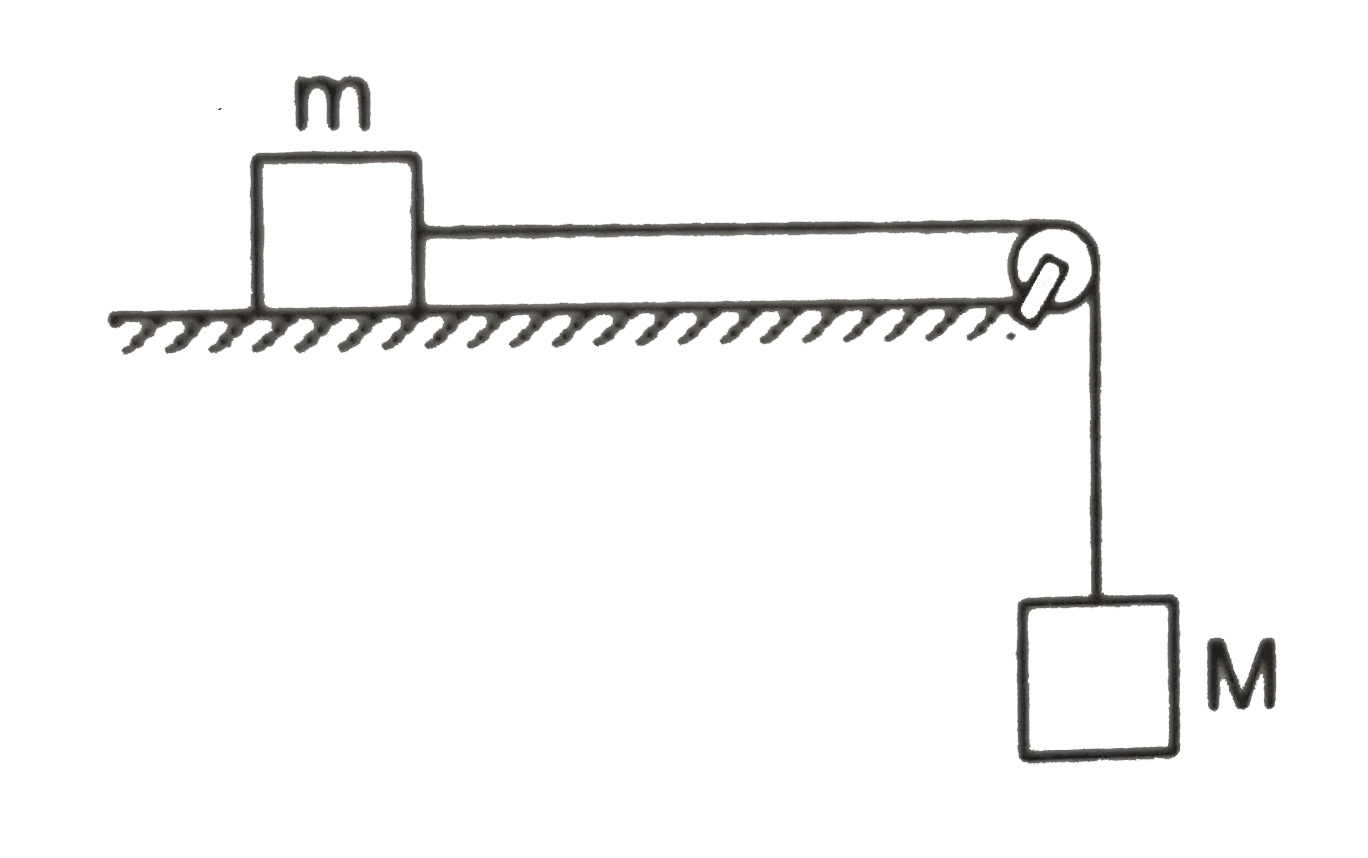
View SolutionTwo blocks are connected by a string that passes over a pulley of radius R and moment of inertia I. The block of mass m1 sides on a frictionless, horizontal surface, the block of mass m2 is suspended from the string. Find the acceleration a of the blocks and the tension T1 and T2 assuming that the string does not slip on the pulley.

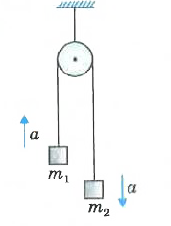
View SolutionString going over a pulley connects two blocks of masses m, and my. String and pulley are light. Calculate acceleration of centre of mass of blocks system.
View SolutionIn the situation shown in figure, both the pulleys and the strings are light and all the surfaces are frictionless. The acceleration of mass M, tension in the string PQ and force exerted by the clamp on the pulley, will respectively be -
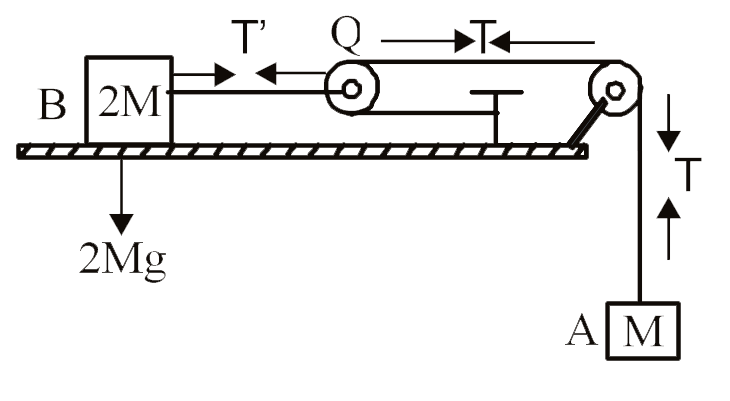
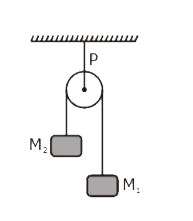
View SolutionIn the figure, the blocks have masses M1andM2(M1>M2) and acceleration a. The pulley P has a radius r and some mass the string not slip on the pulley
View Solution
