The area bounded by the curve $a^{2} y = x^{2} (x + a)$ and the x-axis is

A

$a^{2} / 3$ sq. units

B

$a^{2} / 4$ sq. units

C

$3 a^{2} / 4$ sq. units

D

$a^{2} / 12$ sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

The curve is $y = \frac{x^{2} (x + a)}{a^{2}}$ , which is a cubic polynomial.
Since $\frac{x^{2} (x + a)}{a^{2}} = 0$ has a repeated root x=0, it touchses x-axis at (0,0) and intersects at (-a,0).

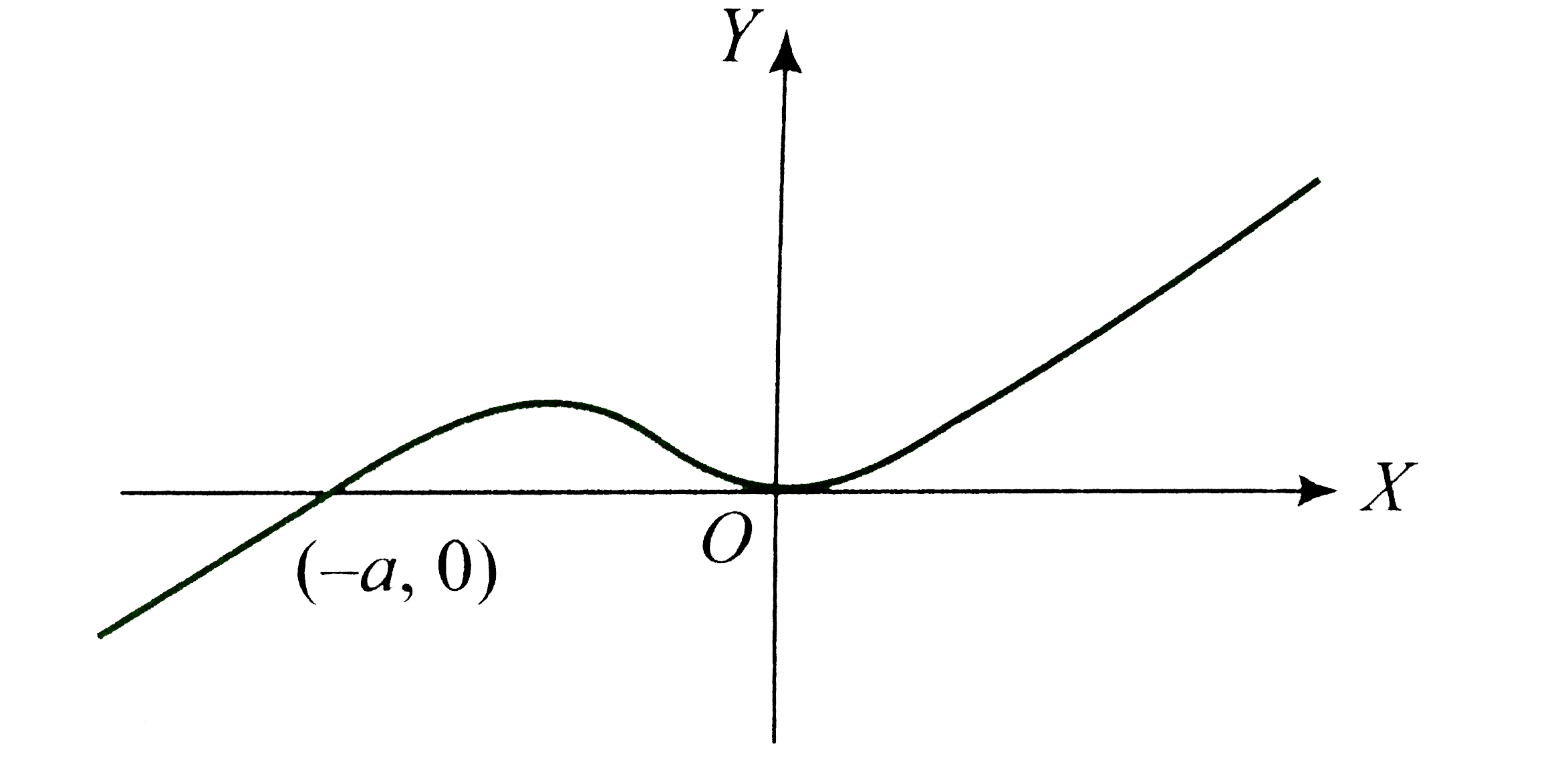
$Required area = \int_{- a}^{0} y d x$
$= \int_{- a}^{0} [\frac{x^{2} (x + a)}{a^{2}}] d x$
$= a^{2} / 12$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curve $y = x^{2} {(x - 1)}^{2}$ with the x - axis is k sq. units. Then the value of 60 k is equal to
A1
B2
C $\frac{1}{2}$
D $\frac{1}{4}$
Question 2 - Select One
The area bounded by the curve $y = {sin}^{2} x - 2 sin x$ and the x-axis, where $x \in [0, 2 π]$ , is
A4 sq. units
B8 sq. units
C16 sq. units
D20 sq. units
Question 3 - Select One
the area included between the curve $x y^{2} = a^{2} (a - x)$ and y -axis is -
A $π a^{2} / 2$
B $π a^{2}$
C $3 π a^{2}$
DNone

CENGAGE-AREA-Exercise (Single)

Home
Ask Doubt
Profile