The area inside the parabola $5 x^{2} - y = 0$ but outside the parabola $2 x^{2} - y + 9 = 0$ is

A

$12 \sqrt{3}$ sq. units

B

$6 \sqrt{3}$ sq. units

C

$8 \sqrt{3}$ sq. units

D

$4 \sqrt{3}$ sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

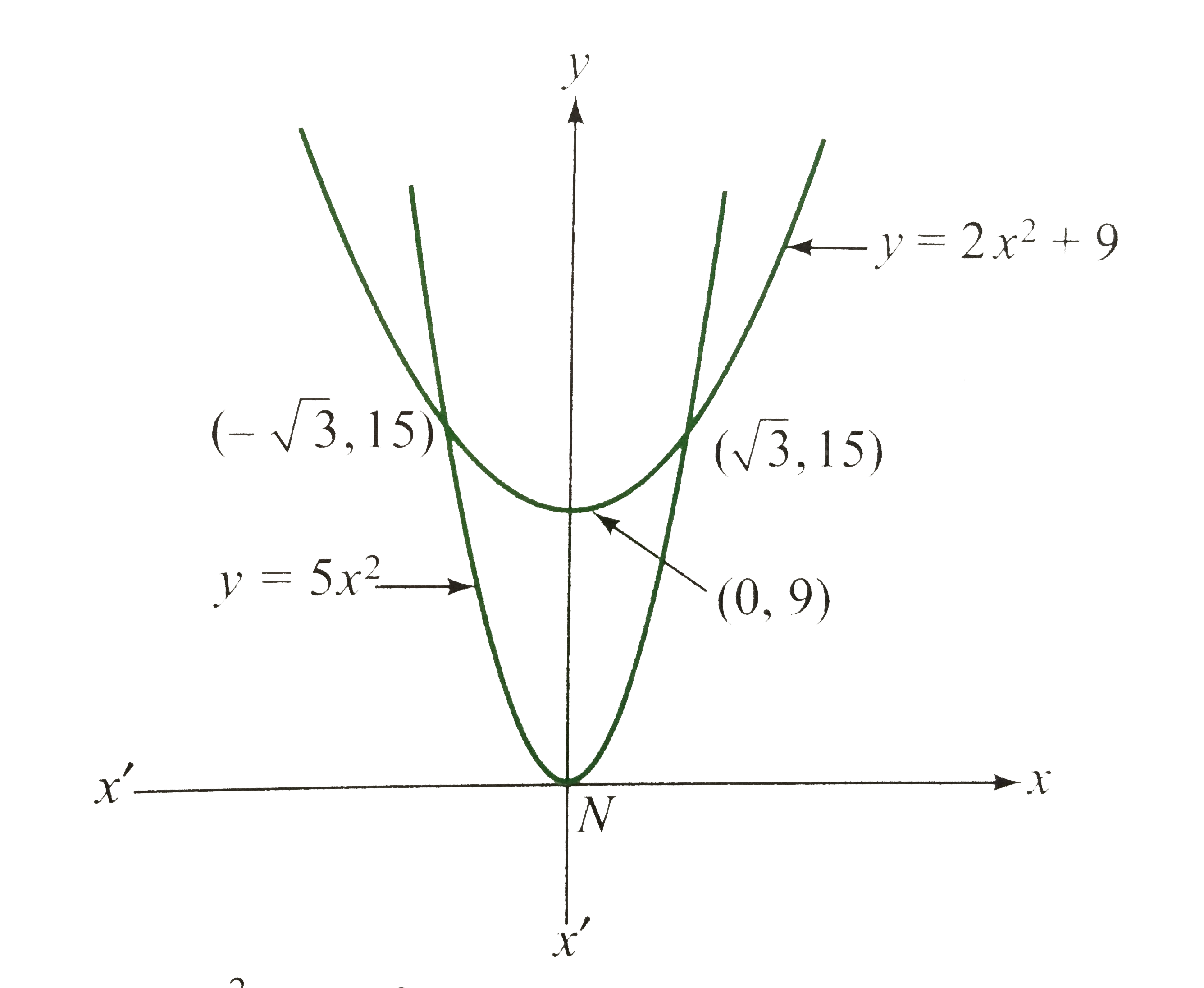
$Given 5 x^{2} - y = 0 ...(1)$
$and 2 x^{2} - y + 9 = 0 ...(2)$
$5 x^{2} - (2 x^{2} + 9) = 0$
$or 3 x^{2} = 9 or x = - \sqrt{3}, \sqrt{3}$
$∴ Required area = 2 \int_{0}^{\sqrt{3}} ((2 x^{2} + 9) - 5 x^{2}) d x$
$= 2 \int_{0}^{\sqrt{3}} (9 - 3 x^{2}) d x$
$= 2 {[9 x - x^{3}]}_{0}^{3}$
$= 2 [9 \sqrt{3} - 3 \sqrt{3}]$
$= 12 \sqrt{3}$ sq. units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The axis of the parabola $y^{2} + 2 x = 0$ is :
A $x = 0$
B $y = 0$
C $x = 2$
D $y = 2$
Question 2 - Select One
The focus of the parabola $y^{2} - x - 2 y + 2 = 0$ is
A $(1 / 4, 0)$
B $(1 / 2)$
C $(3 / 4, 1)$
D $(5 / 4, 1)$
Question 3 - Select One
The focus of the parabola $x^{2} - 8 x + 2 y + 7 = 0$ is
A $(0, - \frac{1}{2})$
B(4,4)
C $(4, \frac{9}{2})$
D $(- 4, - \frac{9}{2})$

CENGAGE-AREA-Exercise (Single)

Home
Ask Doubt
Profile