AB is double ordinate of the hyperbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ such that $Δ A O B$ (where 'O' is the origin) is an equilateral triangle, then the eccentricity e of hyperbola satisfies:

A

$1 < e < \frac{2}{\sqrt{3}}$

B

$e = \frac{2}{\sqrt{3}}$

C

$e = \frac{\sqrt{3}}{2}$

D

$e < \frac{2}{\sqrt{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

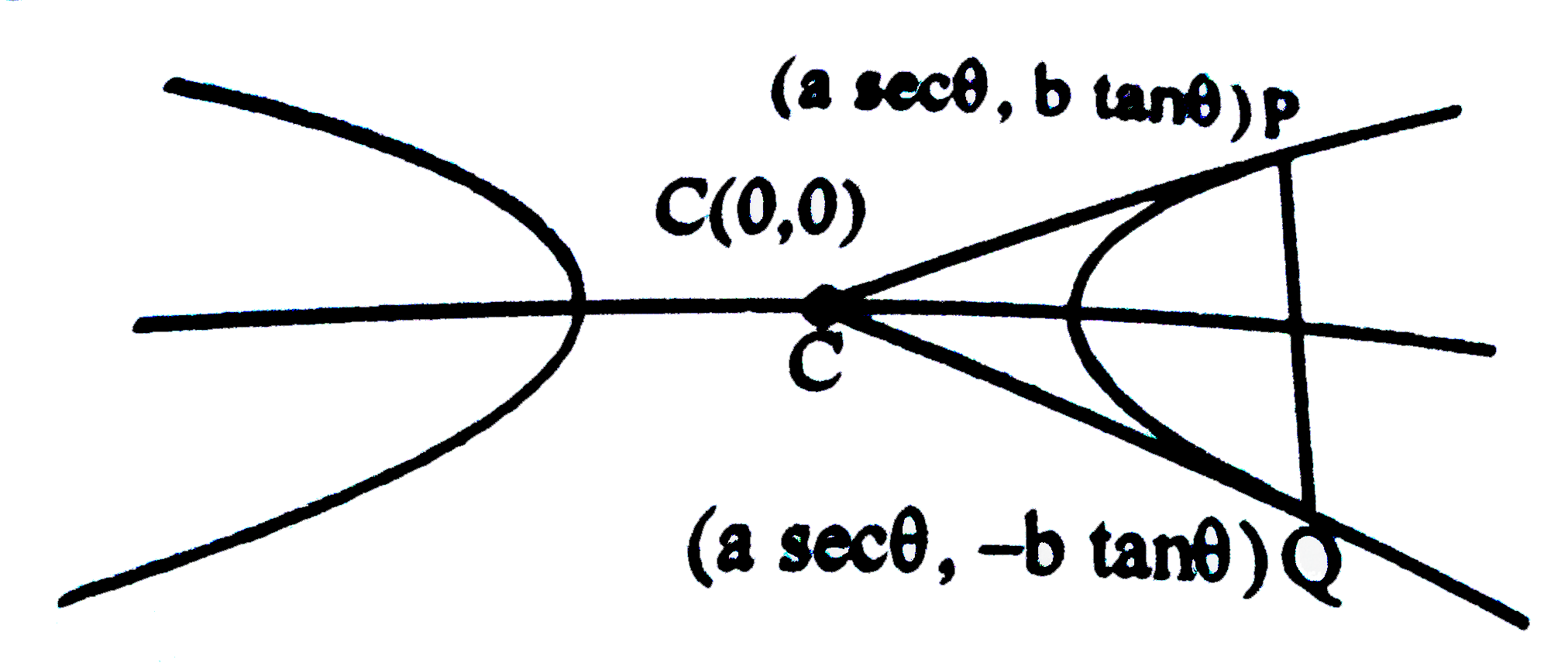
Let the hyperbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ and any double ordinate PQ be (a $sec θ, b tan θ$ ),( $a sec θ, - b tan θ)$ .
O is the centre(0,0).
$Δ O P Q$ is euilateral. So
${tan 30}^{\circ} = \frac{b, tan θ}{a sec θ}$
$\Rightarrow 3 \frac{b^{2}}{a^{2}} = cos e c^{2} θ$
$\Rightarrow 3 (e^{2} - 1) = cos e c^{2} θ$
Now $cos e c^{2} θ \geq 1$
$\Rightarrow 3 (e^{2} - 1) \geq 1 \Rightarrow e^{2} \geq \frac{4}{3} \Rightarrow e > \frac{2}{\sqrt{3}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $P Q$ is a double ordinate of the hyperbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ such that $O P Q$ is an equilateral triangle, $O$ being the center of the hyperbola, then find the range of the eccentricity $e$ of the hyperbola.
A $1 < e < \frac{2}{\sqrt{3}}$
B $e = \frac{2}{\sqrt{3}}$
C $e = \frac{\sqrt{3}}{2}$
D $e > \frac{2}{\sqrt{3}}$
Question 2 - Select One
If PQ is a double ordinate of the hyperbola such that OPQ is an equilateral triangle, being the centre of the hyperbola, then eccentricity e of the hyperbola satisfies
A $e = \frac{2}{\sqrt{3}}$
B $e = \frac{\sqrt{3}}{2}$
C $e > \frac{2}{\sqrt{3}}$
D $1 < e < \frac{2}{\sqrt{3}}$
Question 3 - Select One
The eccentricity of the hyperbola $16 x^{2} - 9 y^{2} = 1$ is?
A $\frac{3}{5}$
B $\frac{5}{3}$
C $\frac{4}{5}$
D $\frac{5}{4}$

BANSAL-TEST PAPERS-MATHS

Home
Ask Doubt
Profile