Two small -sized identical equally charged spheres each having mass 1 mg are hanging in equilibrium as shown in the figure . The length of each string is 10 cm and the angle is with the vertical . Calculate the magnitude of the charge in each sphere . (Take g =
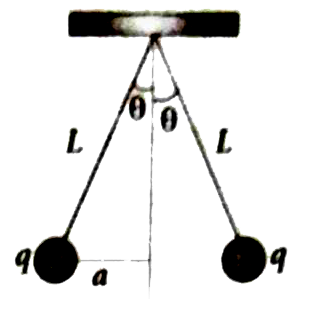
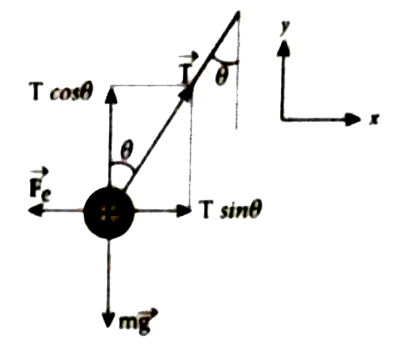
If the spheres are neutral the angle between them will be when hanged vertically . Since they are positively charged spheres , there will be a repulsive force between them and they will be at equilibrium with each other at an angle of with the vertiction. We can draw a free body diagram for one of the charged spheres and apply Newton.s second law for both vertical and horizontal directions . The free body diagram is shown. In the x -direction the acceleration of the charged sphere is zero . Using Newton.s second law , we have T sin
T
Here T is the tension acting on the charge due to the string and is the electrostatic force between the two charges . In the y -direction also the net acceleration experienced by the charge is zero . T
Therefore T cos . By dividing equation (1) by equation (2) ,
Since they are equally charged the magnitude of the electrostatic force is
where k
Here r = 2a = 2L . By substituting these values in equation (3) ,
Rearranging the equation (4) to get q
Topper's Solved these Questions
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (Multiple choice questions : )
15 Videos
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (II. Short Answer Questions : )
21 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - FULL MARKSCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )
10 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
4 Videos
Similar Questions
Two identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the ligth of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
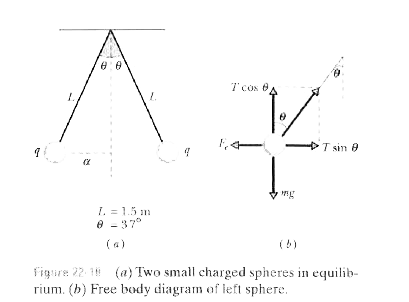
View SolutionTwo identical, small, charged spheres, each having a mass of 4.0×10−2kg hang in equilibrium as shown in Fig. 22-10a. The length of each string is 1.5m and the angle θ is 37.0∘. Find the magnitude of the charge on each sphere.
View Solution
Knowledge Check
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3
Two identical small charged spheres, each having a mass m, hang in equilibrium the length of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
View SolutionTwo identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionThree identically charged, small spheres each of mass m are suspended from a common point by insulated light strings each of length I. The spheres are always on vertices of an equilateral triangle of length of the sides x(<<l). Calculate the rate dq/ dt with which charge on each sphere increases if length of the sides of the equilateral triangle increases slowly according to law dxdt=a√x
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo identical charges repel each other with a force equal to 1mg wt when they are 0.6m apart in air.The value of each charge is (g=10ms−2 )
View SolutionTwo identical helium filled balloons A and B fastened to a weight of 5 g by threads floats in equilibrium as shown in figure. Calculate the charge on each balloons, assuming that they carry equal charge.
View Solution
