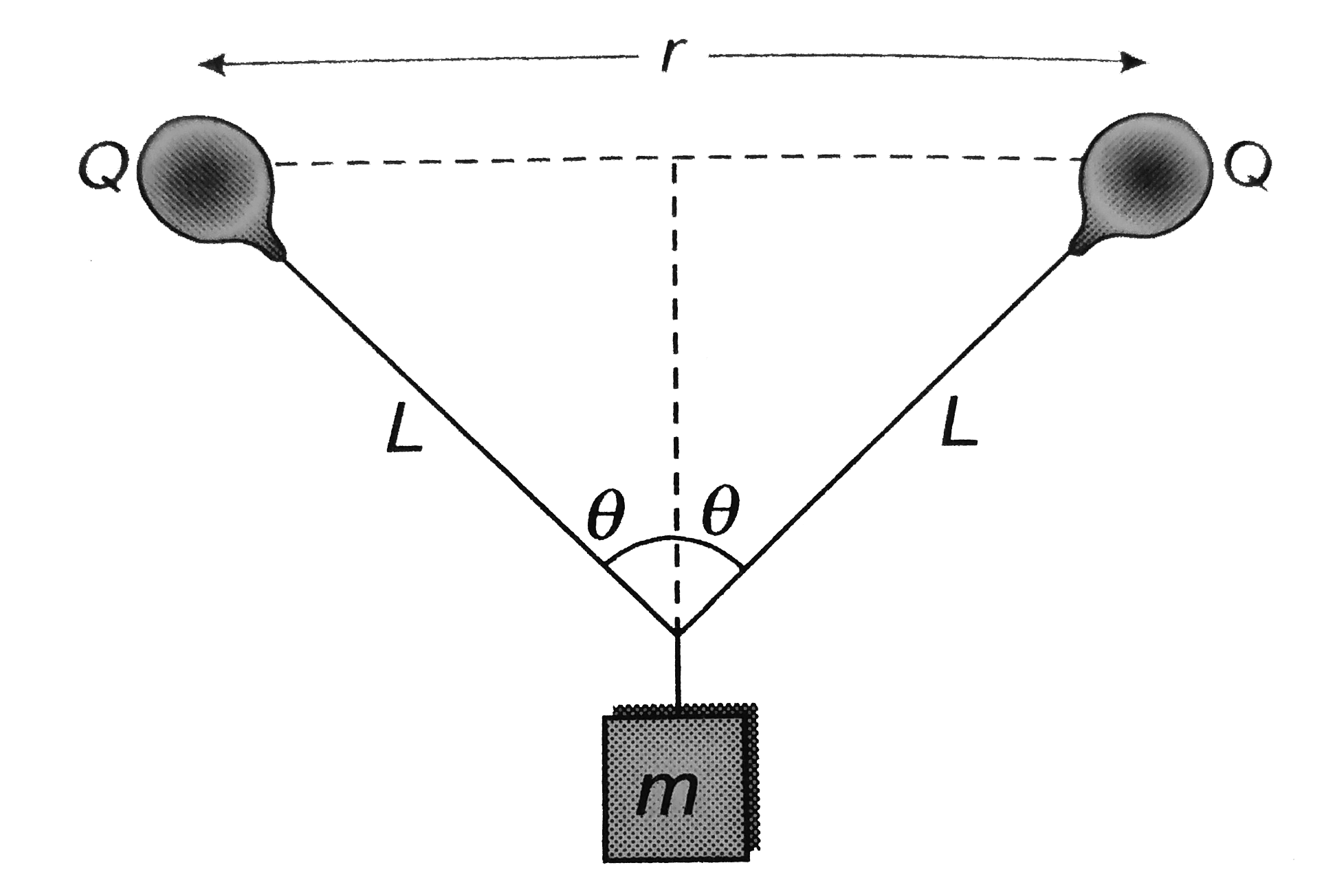
Two identical helium filled balloons A and B fastened to a weight of 5 g by threads floats in equilibrium as shown in figure. Calculate the charge on each balloons, assuming that they carry equal charge.
To solve the problem of calculating the charge on each helium-filled balloon A and B, we will follow these steps:
Step 1: Understand the Forces Acting on the Balloons
The balloons are in equilibrium, meaning that the forces acting on them are balanced. The forces include:
- The gravitational force acting downwards (weight of the balloons).
- The tension in the threads acting upwards.
- The electrostatic repulsive force between the two charged balloons acting horizontally.
Step 2: Calculate the Weight of the Balloons
The weight W of the balloons can be calculated using the formula:
W=m⋅g
where:
- m=5g=0.005kg (mass of the balloons),
- g=10m/s2 (acceleration due to gravity).
Calculating the weight:
W=0.005kg⋅10m/s2=0.05N
Step 3: Set Up the Equations of Equilibrium
Let T be the tension in the thread. For the vertical forces, we have:
2Tcos(θ)=W
For the horizontal forces, we have:
Tsin(θ)=F
where F is the electrostatic force between the two charged balloons.
Step 4: Relate the Forces
From the equilibrium conditions, we can express F in terms of W and θ:
F=Wtan(θ/2)
Step 5: Calculate the Electrostatic Force
The electrostatic force F between two charges q separated by a distance r is given by Coulomb's law:
F=kq2r2
where k=9×109N m2/C2 (Coulomb's constant).
Step 6: Combine the Equations
Equating the two expressions for F:
Wtan(θ/2)=kq2r2
Step 7: Solve for Charge q
Rearranging the equation gives:
q2=Wtan(θ/2)r2k
Taking the square root gives:
q=√Wtan(θ/2)r2k
Step 8: Substitute the Known Values
Assuming r is the distance between the two balloons, and substituting the known values:
- W=0.05N
- r=0.6m (assuming a distance of 0.6 m between the balloons)
- k=9×109N m2/C2
- tan(θ/2)=0.3 (as given in the transcript)
Substituting these values into the equation for q:
q=√0.05⋅0.3⋅(0.6)29×109
Step 9: Calculate the Charge
Calculating the value:
q=√0.05⋅0.3⋅0.369×109=√0.00549×109=√6×10−13≈5.6×10−7C
Final Answer
The charge on each balloon is approximately:
q≈5.6×10−7C
---
The balloons are in equilibrium, meaning that the forces acting on them are balanced. The forces include:
- The gravitational force acting downwards (weight of the balloons).
- The tension in the threads acting upwards.
- The electrostatic repulsive force between the two charged balloons acting horizontally.
The weight W of the balloons can be calculated using the formula:
W=m⋅g
where:
- m=5g=0.005kg (mass of the balloons),
- g=10m/s2 (acceleration due to gravity).
W=0.005kg⋅10m/s2=0.05N
Let T be the tension in the thread. For the vertical forces, we have:
2Tcos(θ)=W
For the horizontal forces, we have:
Tsin(θ)=F
where F is the electrostatic force between the two charged balloons.
From the equilibrium conditions, we can express F in terms of W and θ:
F=Wtan(θ/2)
The electrostatic force F between two charges q separated by a distance r is given by Coulomb's law:
F=kq2r2
where k=9×109N m2/C2 (Coulomb's constant).
Equating the two expressions for F:
Wtan(θ/2)=kq2r2
Rearranging the equation gives:
q2=Wtan(θ/2)r2k
Taking the square root gives:
q=√Wtan(θ/2)r2k
Assuming r is the distance between the two balloons, and substituting the known values:
- W=0.05N
- r=0.6m (assuming a distance of 0.6 m between the balloons)
- k=9×109N m2/C2
- tan(θ/2)=0.3 (as given in the transcript)
q=√0.05⋅0.3⋅(0.6)29×109
Calculating the value:
q=√0.05⋅0.3⋅0.369×109=√0.00549×109=√6×10−13≈5.6×10−7C
The charge on each balloon is approximately:
q≈5.6×10−7C
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two identical He-filled spherical balloons each carrying a charge q are tied to a weight W with strings and float in equlibrium, as shown in figure.
(i) Find the magnitude of q, assuming that the charge on each balloon acts as if it were concentrated at the center.
(ii) Find the volume of each balloon. Take the density of He as ρHe and the density of air as ρa. Ignore the weight of the unfilled balloons .
 ,
,
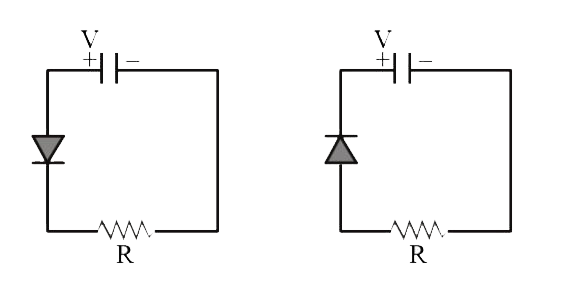
View SolutionTwo identical capacitors A and B are charged to the same potential V and are connected in two circuits at t = 0 as shown in figure. The charge of the capacitors at a time t = CR are respectively -
View SolutionTwo similar balloons filled with helium gas are tied to Lm long string. A body of mass m is tied to another ends of the strings. The balloons float on air at distance r. If the amount of charge on the ballons is same then the magnitude of charge on each balloon will be
View Solution_E01_093_Q01.png)
A ballong filled with air is weighted so that it barely floats in water as shown in figure. When it is pushed down so that it gets submerged a short distance in water then the balloon
View SolutionTwo identical small equally charged conducting balls are suspended from long threads secured at one point. The charges and masses of the balls are such that they are in equilibrium when the distance between them is a(the length of thread L>>a). Then one of the balls is discharged. what will be the distance b(b<<L) between the balls when equilibrium is restored?
View SolutionA and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then
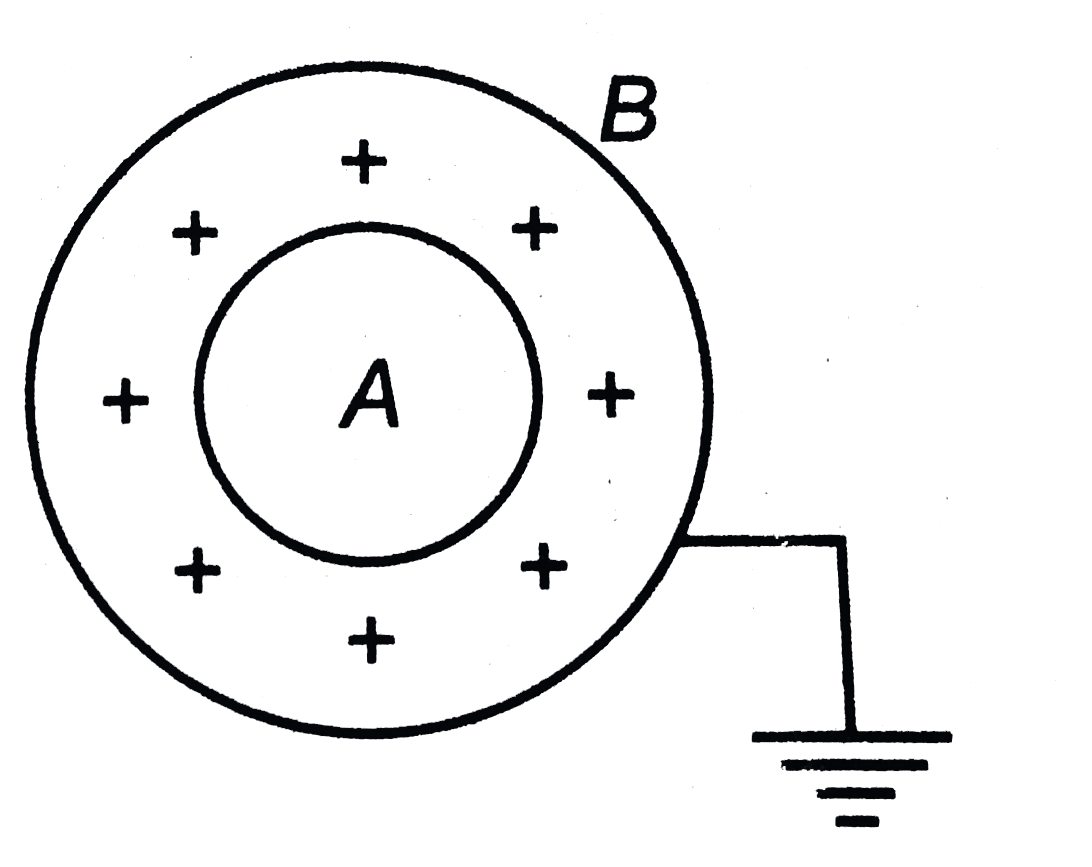
View SolutionA and B are two concentric spherical shells. If A is given a charge +Q while B is earthed as shown in figure then

View SolutionIn the circuit shown in figure find
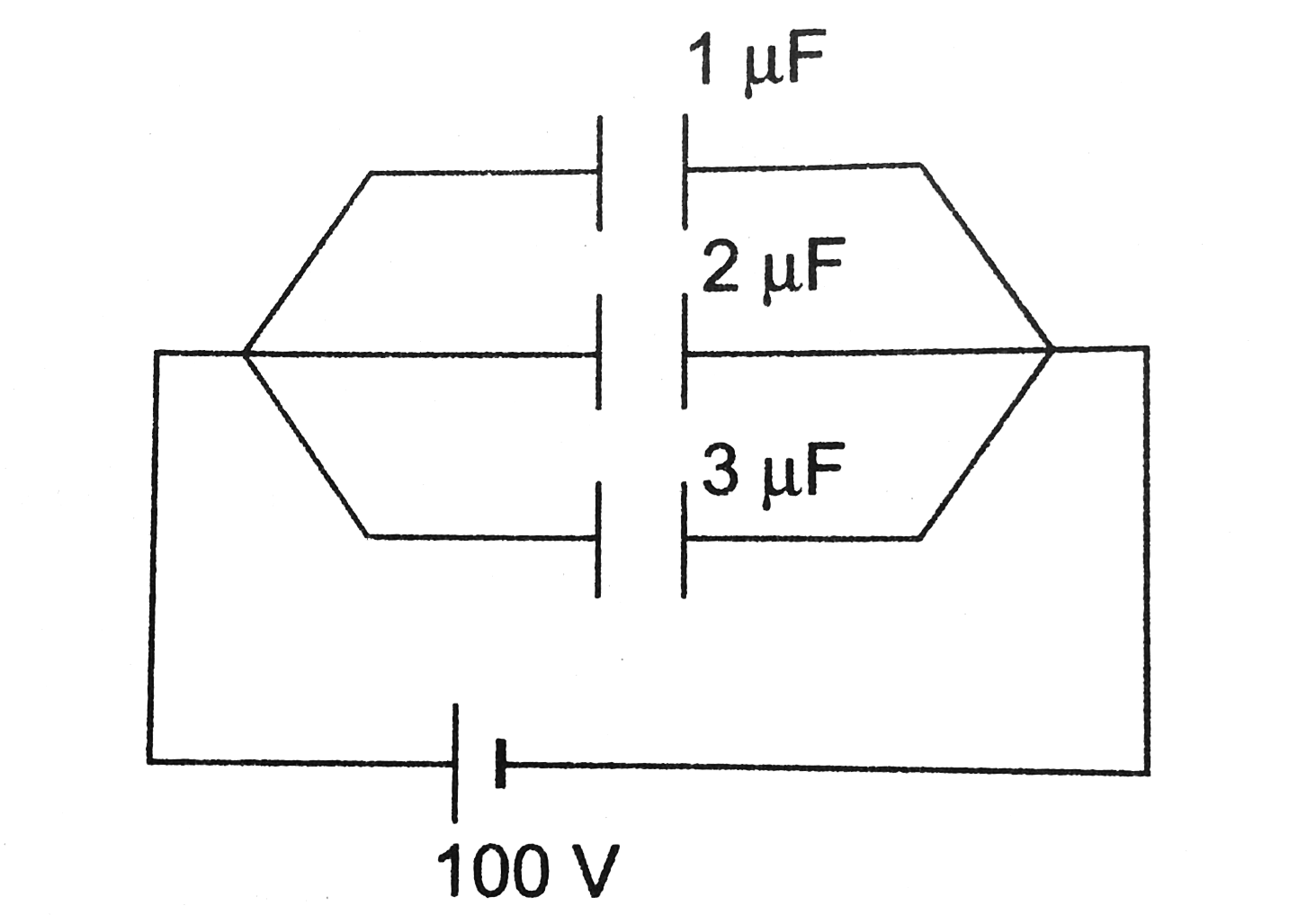
a. the equivalent capacitance and
b. the charge stored in each capacitor.
View SolutionIn the circuit shown in figure find

a. the equivalent capacitance and
b. the charge stored in each capacitor.
View SolutionIn the circuit shown in figure find

a. the equivalent capacitance and
b. the charge stored in each capacitor.
View Solution
