ABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన (ABCD)వై||=ABxDG వై|| అని చూపండి.
Step by step video & image solution for ABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన (ABCD)వై||=AB x DG వై|| అని చూపండి. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
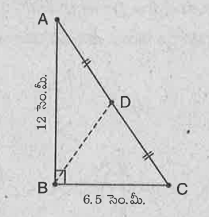
△ABC లో ∠ABC=90∘, AD=DC, AB=12 సెం.మీ. మరియు BC=6.5 సెం.మీ. అయిన △ADB వైశాల్యము కనుగొనండి.
View Solutionపటంలో O వృత్త కేంద్రం. ఆయన దిగువ ఇవ్వబడిన భాగాల పేర్లు తెలపండి.
 ¯¯¯¯¯¯AO
¯¯¯¯¯¯AO
View Solutionఒక నాణెన్నీ 100 సార్లు ఎగురవేసినప్పుడు పర్యవసానాలు కింది విధంగా ఉన్నాయి. బొమ్మ : 45 సార్లు , బొరుసు : 55 సార్లు అయిన . ప్రతి పర్యవసానం యొక్క సంభావ్యత కనుక్కోండి.
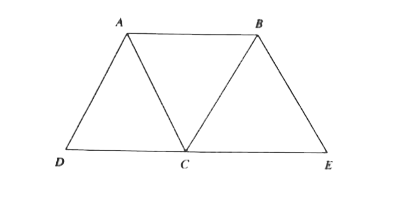
View SolutionIn the figure, ABCD and ABEF are parallelograms. The area of the quadrilateral ABED is 6. what is the area of the parallelogram ABCD?
View Solutionಸಮಾಂತರ ಚತುರ್ಭುಜ ABCD ಮತ್ತು ABEF ಆಯತಗಳು AB ಪಾದದ ಮೇಲಿದ್ದು ವಿಸ್ತೀರ್ಣಗಳು ಸಮನಾಗಿವೆ. ಆದರೆ ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಸುತ್ತಳತೆಯು ಆಯತದ ಸುತ್ತಳತೆಗಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
View Solutionsquare ABCD In the trapezium AB // CD . /_A=45^@ అయిన /_D =
View SolutionABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన (ABCD)వై||= (ABEF) వై|| అని చూపండి.
View SolutionA={x : x ∈ N x < 6} మరియు B={x : x ∈ N మరియు 3<x<8}అయినA−B!= B - A అని వెన్ చిత్రాల ద్వారా చూపండి.
View SolutionPrice of 5 pens and 3 pencils p Price of Rs., 3 pens and 2 pencils q' రూ॥1లు అయిన 2 పెన్నులు మరియు ఒక పెన్సిల్ ధర = ............. రూ॥
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
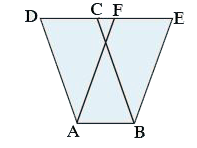
View SolutionThe area of parallelogram ABCD is 36cm2 . Calculate the height of parallelogram ABEF if AB = 4.2 cm
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solution
