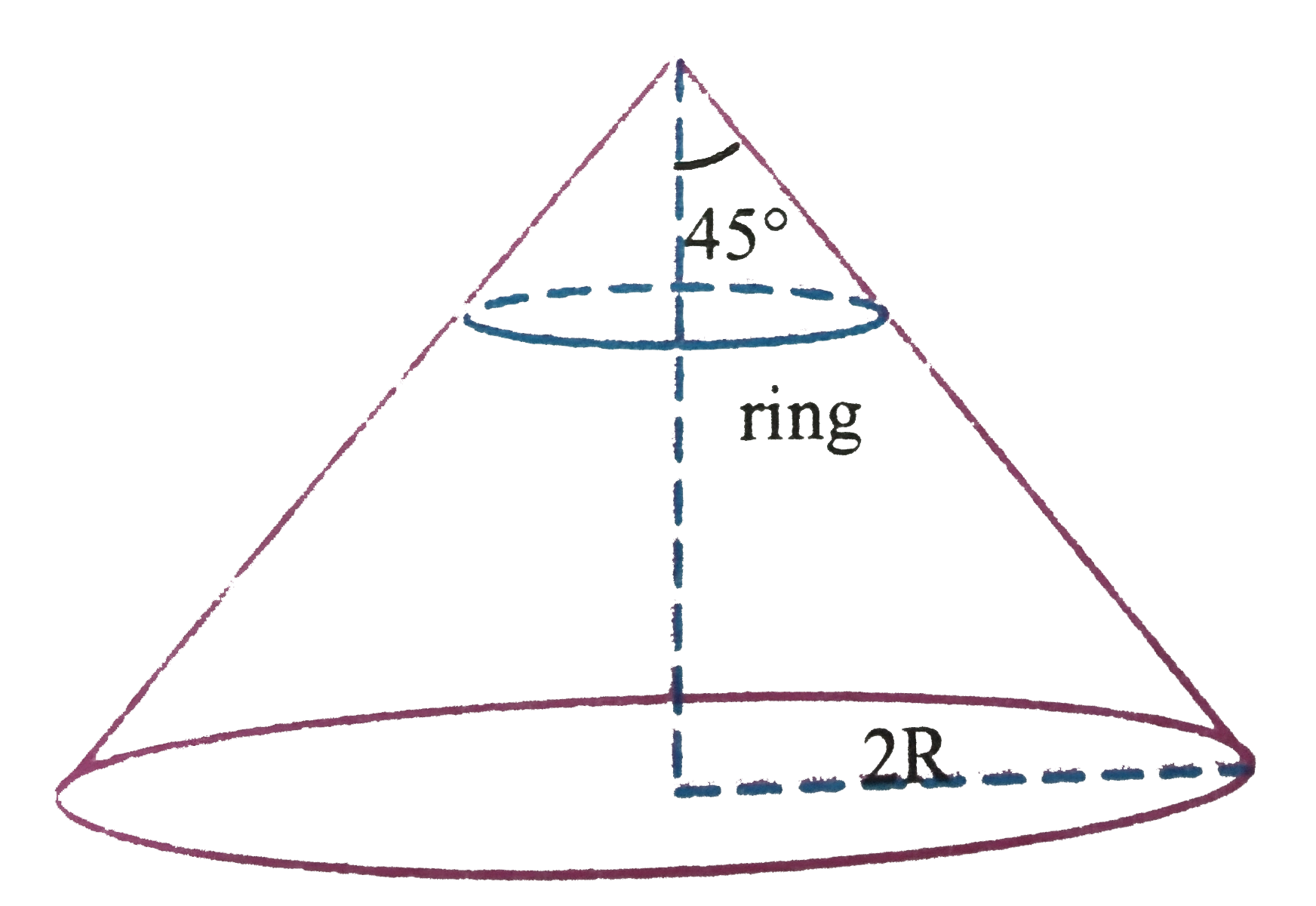
A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle 45∘ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is r(r<<R).
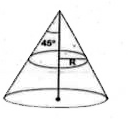
What will be the tension in the ring?
mg2√2π
mg2π
mg√2π
√2mgπ
The correct Answer is:B
FBD of small section of ring subtending angle dθ at centre of ring is as shown.
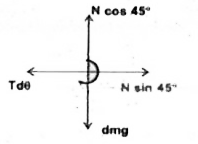
N√2=Tdθ,N√2=mdθ2πg
⇒T=mg2π
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSERTION REASONING TYPE
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - NUMERICAL BASED QUESTIONS
5 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION - I
6 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
Knowledge Check
A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle 45∘ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is r(r<<R).
What will be the speed of transverse wave on the ring?A√gRB√2gRC12√gRD2√gRFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA unifrom metallic ring of mass m, radisus R, cross sectional area 'a' and young'/s modulus Y kis kept on a smooth cone of radius 2R and semivertex angle 45∘ as shown. [Assume that extension in the ring is small]
 AThe tension in the ring will be same through outBThe tension in the ring will be independent of radius of ring.CThe extension in the ring will be mgRaYDElastic potential energy should in the ring will be m2g2R8πYa
AThe tension in the ring will be same through outBThe tension in the ring will be independent of radius of ring.CThe extension in the ring will be mgRaYDElastic potential energy should in the ring will be m2g2R8πYa
A chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
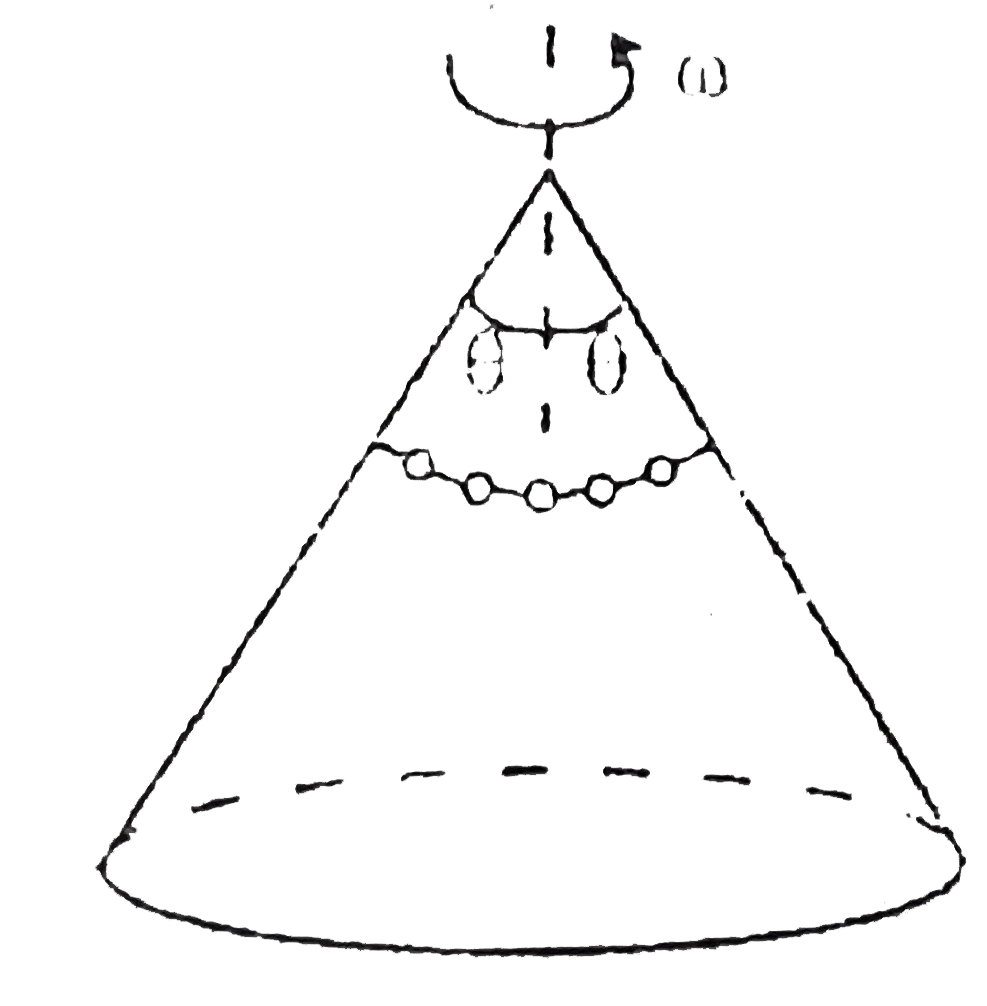
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
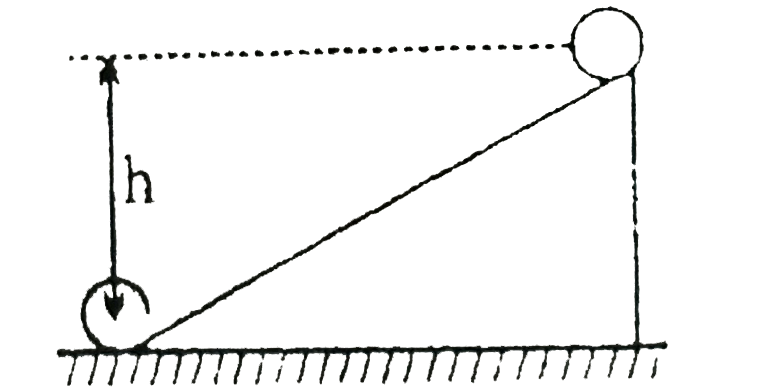
View SolutionA ring of mass M and radius R is at rest at the top of an incline as shown. The ring rolls down the plane without slipping. When the ring reaches bottom, its angular momentum about its centre of mass is:
View SolutionA ring of mass M and radius R is released on an inclined as shown. If the coefficient of friction μ<12tanθ, then during a displacement l:
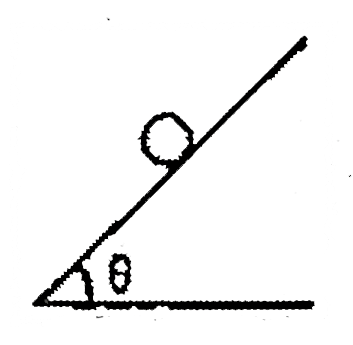
View SolutionConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
View Solution
