A uniform vertical cylinder of cross-sectional area 'a' floats, 90% submerged, in an unknown liquid inside a tank -with cross-sectional area four times that of cylinder. When cylinderis pushed down gently and released it performs SHM. The maximum possible amplitude (in cm) for this SHM is
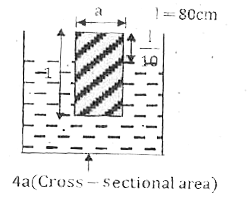
Cylinder can perform SHM only till it is partially submersed. When cylinder goes down x in ground from liquid level comes up by x.. (say).
(4a−a)x.=xa⇒x.=x/3
So the centre of the cylinder goes down by (w.r.t. the liquid surface)
(x+x.)=43x≤110⇒x≤3l40=6cm
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Subjective)
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
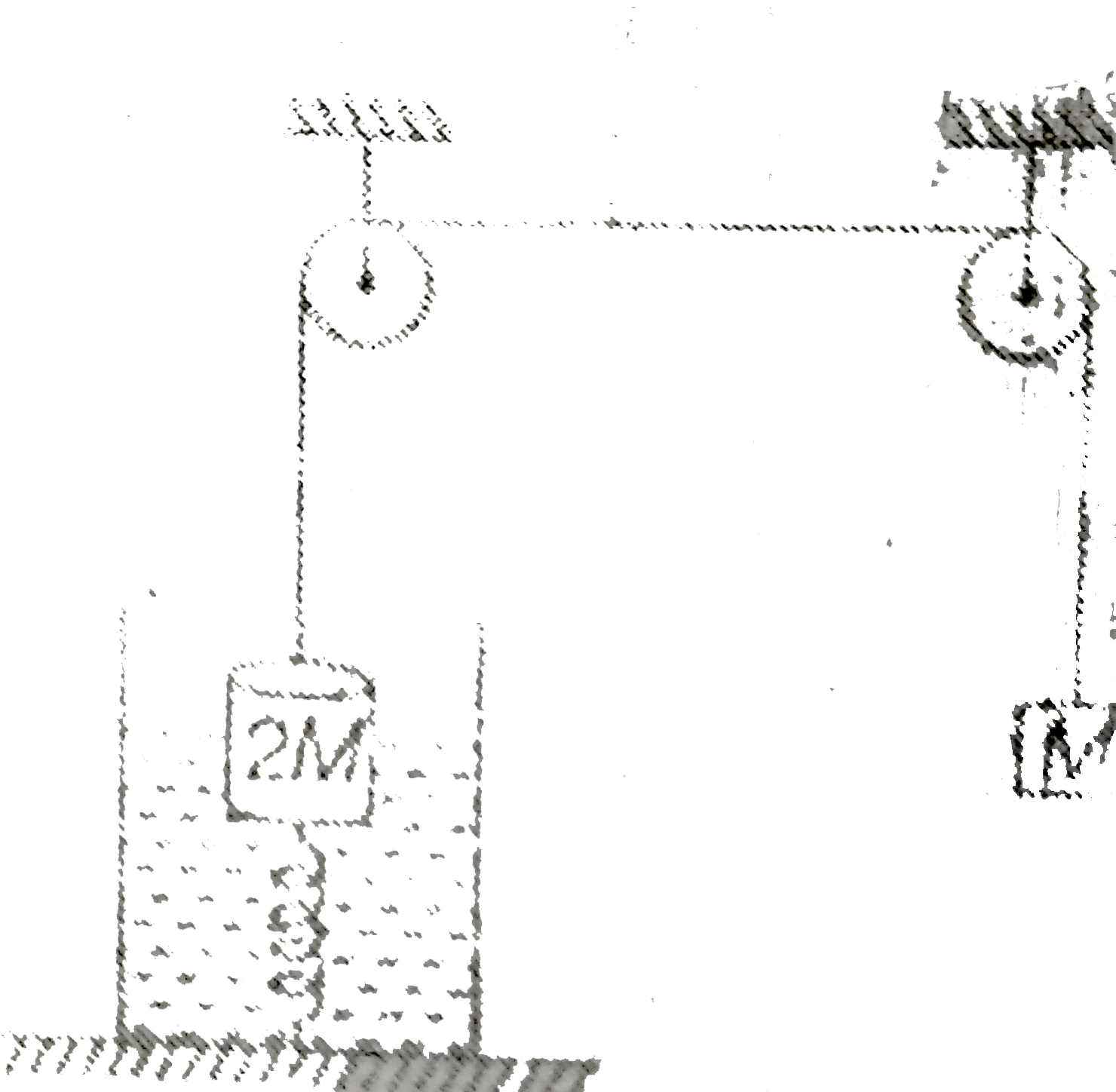
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]
View Solution
Knowledge Check
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

Under equilibrium conditionsAextensions of the spring is Mg3KBcompression of the spring is 2Mg3KCcompression of the spring is Mg8k)Dextension of the spring is Mg6kPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]A3MgK+AρgB3Mg2(K+Aρg)C8Mg3(K+Aρg)D3Mg2K+3AρgPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
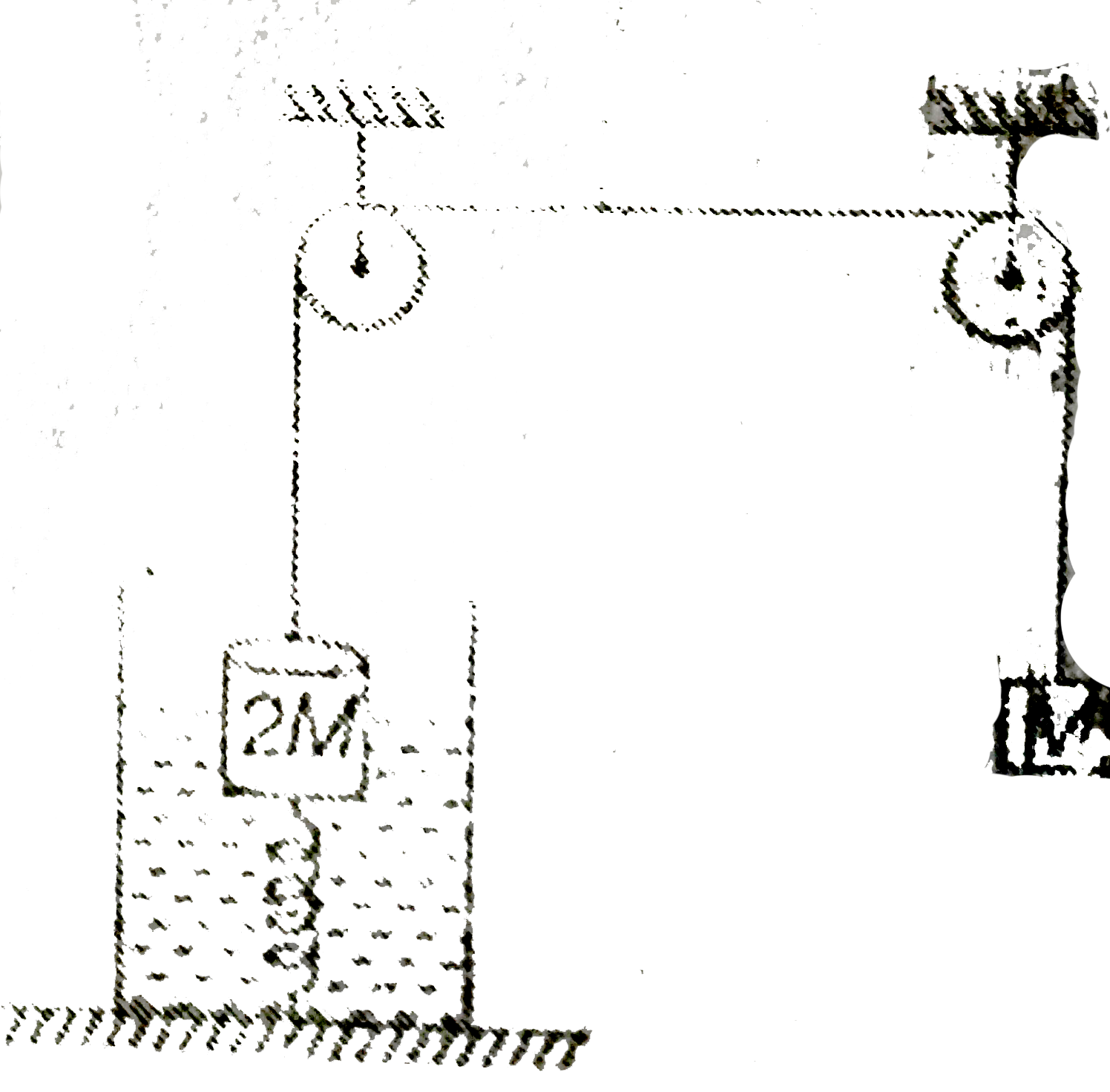
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.A(2pisqrt((3M)/(2(K+Arhog)B(2π√M2K+AρgC2π√3MK+AρgD2π√2MK+3Aρg
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
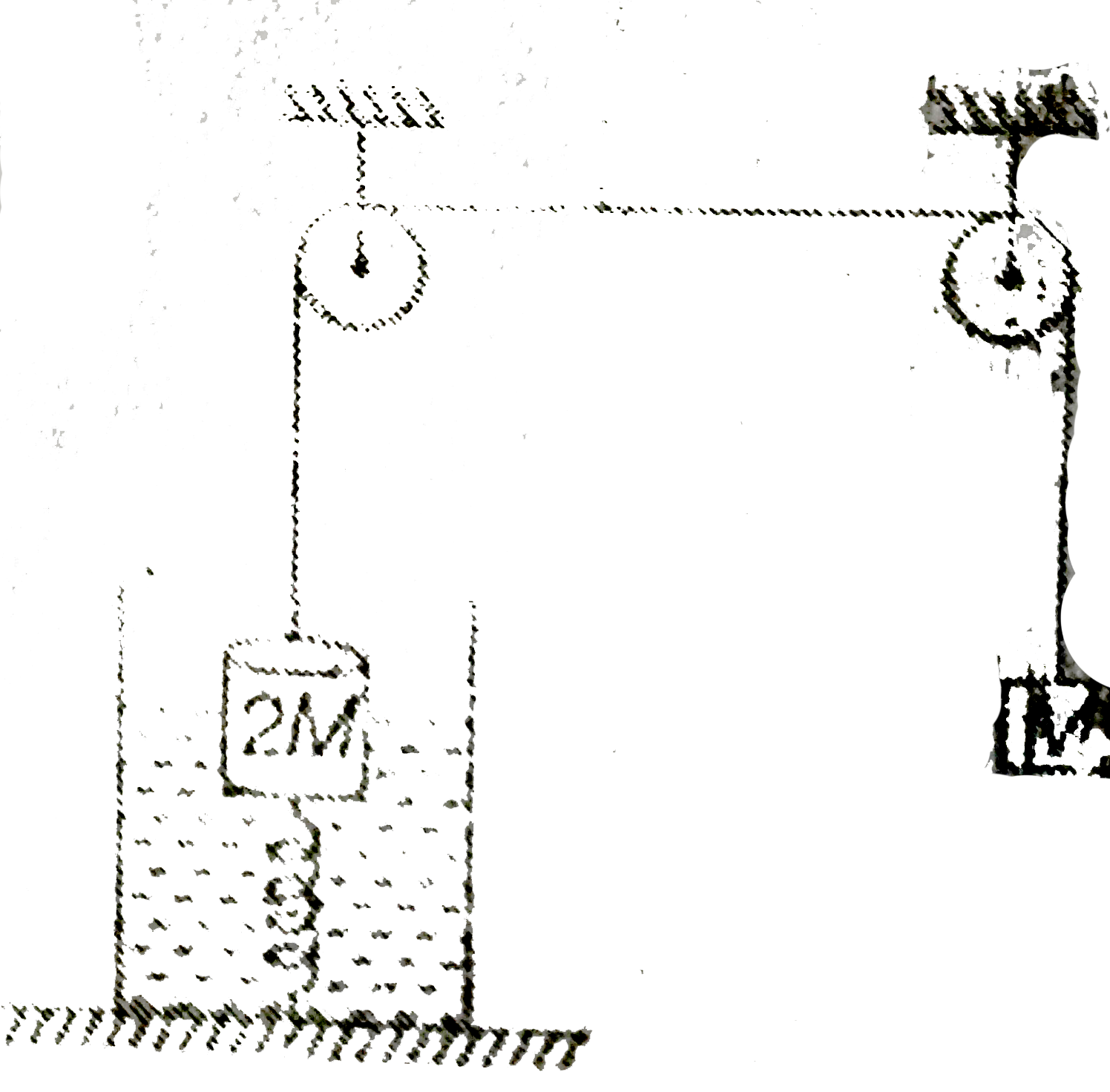
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.
View SolutionA solid cylinder of denisty ρ0, cross-section area A and length l floats in a liquid ρ(>ρ0 with its axis vertical, . If it is slightly displaced downward and released, the time period will be :
View SolutionA solid cylinder of denisty ρ0, cross-section area A and length l floats in a liquid ρ(>ρ0 with its axis vertical, as shown. If it is slightly displaced downward and released, the time period will be :

View SolutionA body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be :
View SolutionA body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be :
View Solution
