In the given figure, (not to scale), rectangle ABCD and triangle ABE are inscribed in the circle O. If ∠AEB=40∘,then find ∠BOC.
A
60∘
B
80∘
C
100∘
D
90∘
Text Solution
The correct Answer is:C
i) Join OA and use properties of arcs.
ii) ∠AOB=2∠AEB.
iii) AOC is the diameter, i.e., ∠AOB+∠BOC=180∘.
|
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Knowledge Check
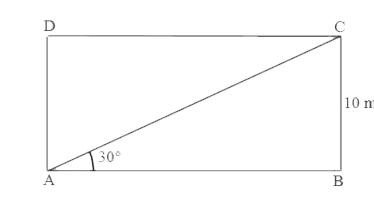
In the given figure, what is the length of AB in rectangle ABCD?
 A8 cmB10 cmC12 cmD16 cm
A8 cmB10 cmC12 cmD16 cmIn the given figure (not to scale ) , O is the centre of the circle . A ,B,C and D are conyclic and AB =CD . If ∠MON=120∘ , then find ∠OPN .
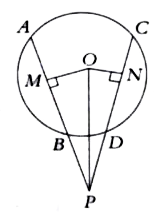 A20∘B30∘C40∘D60∘
A20∘B30∘C40∘D60∘
In the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠BOC
View Solution
In the figure above (not to scale), AB is the diameter of the circle with centre O. If ∠ACO=30∘, then find ∠BOC.
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠OBC
View SolutionIn the given figure (not to scale), O is the center of the circle. If PB=PC, ∠PBO−25∘ and ∠BOC−130∘, then find ∠ABP+∠DCP.

View SolutionIn the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOC
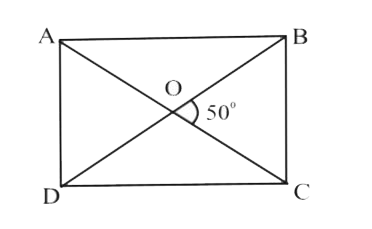
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=50∘ then find ∠ODA.
View Solution