The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
dQdt=k(T1−T2)LA
dQdt=kLA(T1−T2)
dQdt=kA(T1−T2)L
dQdt=kL(T1−T2)A
The correct Answer is:C
dQdt=kA(T1−T2)L
[(T1−T2) is the temperature difference]
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-1: Concept Builder (Topicwise)
69 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- THERMODYNAMICS BOOK - DISHA PUBLICATIONCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE -2 : CONCEPT APPLICATOR
29 Videos
Similar Questions
Two ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by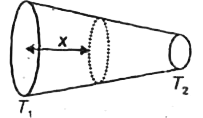
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
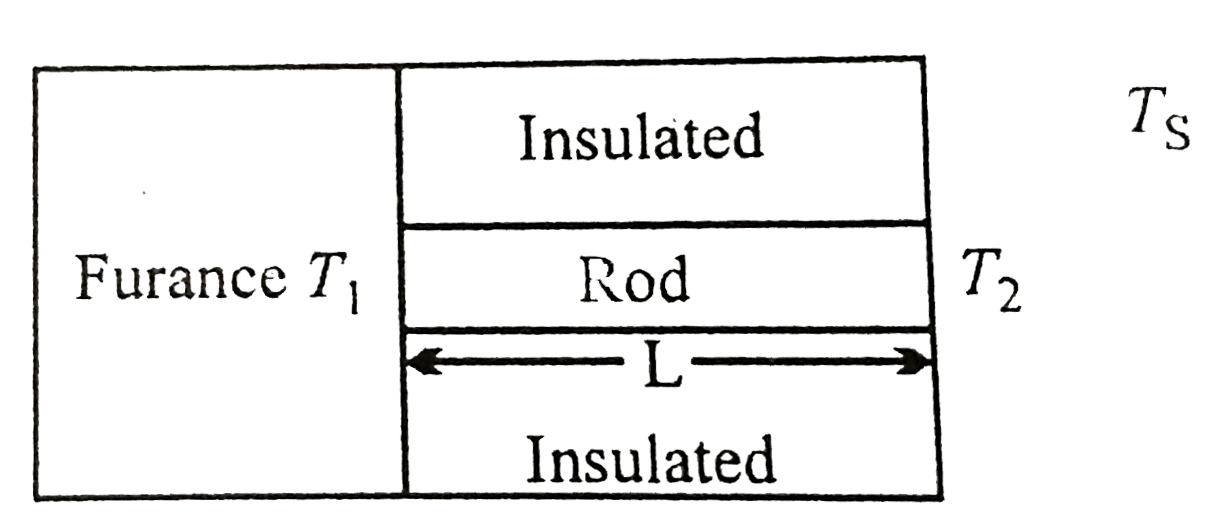
View Solution
Knowledge Check
A black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
Amore atT1Bmore at T2Cequal for T1 and T2Dindependent of T1 and T2A black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
Amore atT1Bmore at T2Cequal for T1 and T2Dindependent of T1 and T2
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod isA√7T0B√5T0C2T0D√3T0
Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionTwo curves are given at temperatures T1andT2 in an isothermal process, then-
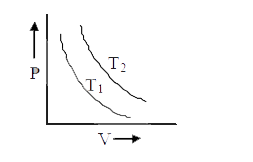
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
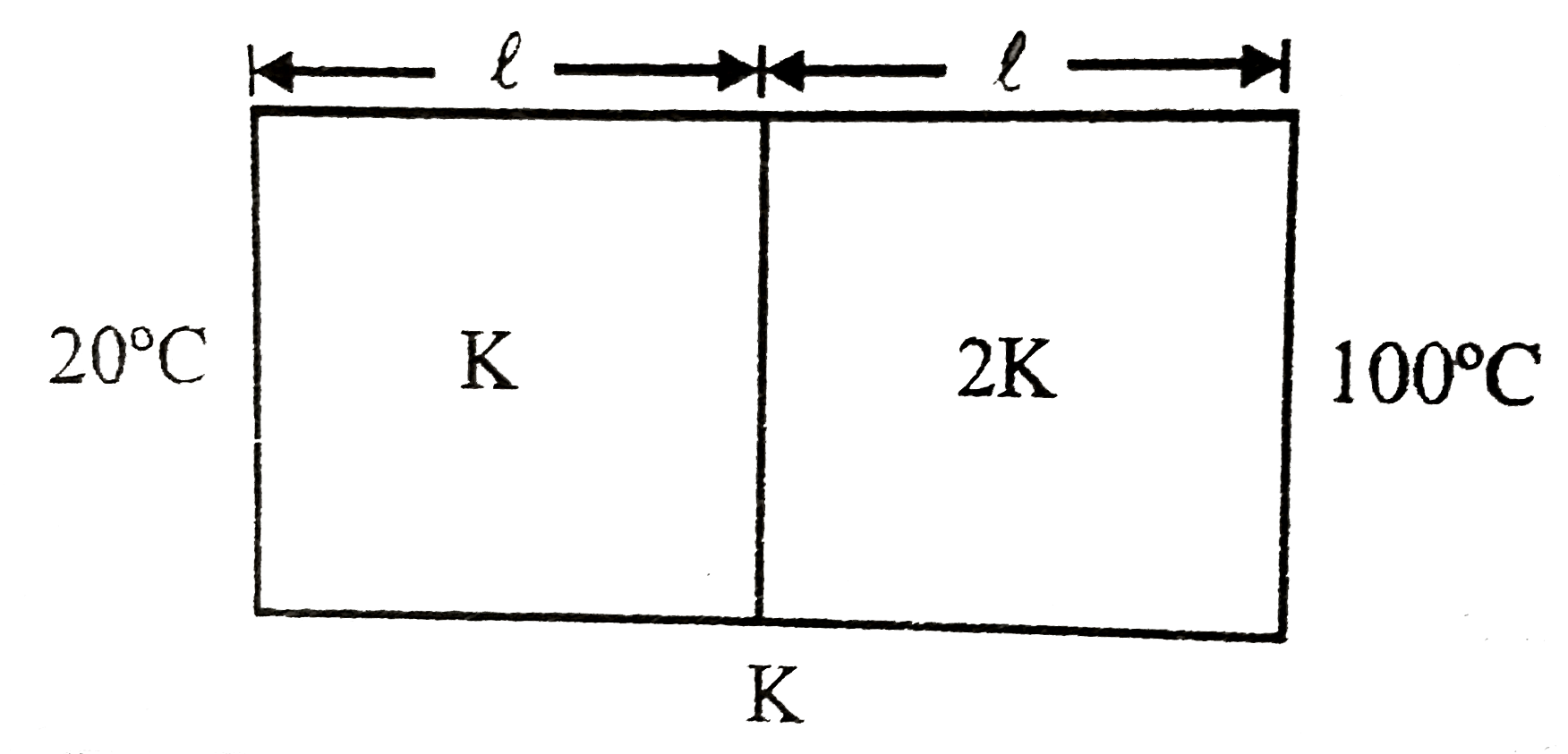
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
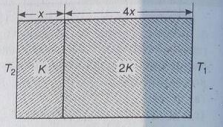
View Solution
