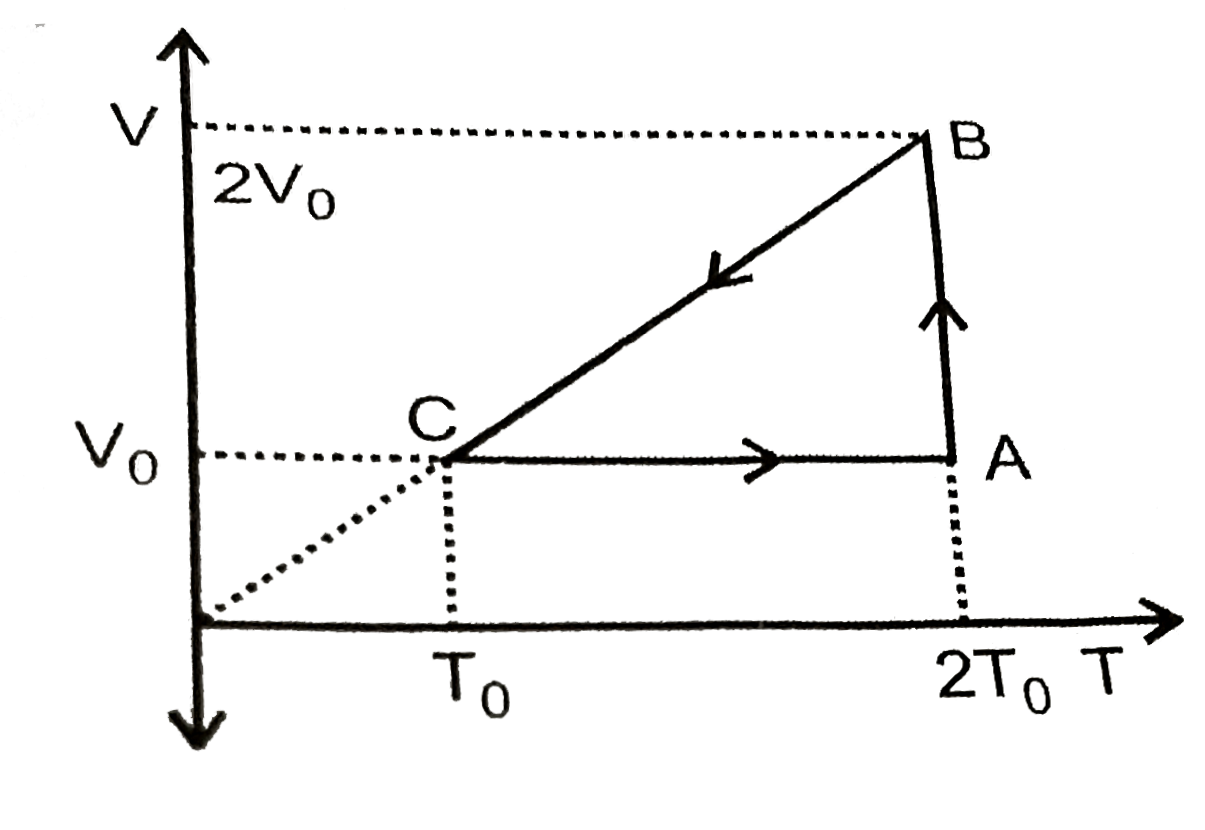
The efficiency of an ideal gas with adiabatic exponent 'y' for the shown cyclic process would be:

A

$\frac{2 ln 2 - 1}{γ / (γ - 1)}$

B

$\frac{1 - 2 ln 2}{γ / (γ - 1)}$

C

$\frac{2 ln 2 + 1}{γ / (γ - 1)}$

D

$\frac{2 ln 2 - 1}{γ / (γ + 1)}$

Text Solution

Verified by Experts

The correct Answer is:A

$W_{A B} = 0, W_{B C} = P Δ V = n R Δ T = - n R T_{0}$
$W_{C A} = n R T \frac{{ln V}_{f}}{V_{i}} = n R (2 T_{0}) ln 2$
$Q_{B C} = n C_{a} Δ T = \frac{n R γ}{γ - 1} T_{0}$
Efficiency, $η = W Q = [\frac{2 ln 2 - 1}{γ / (γ - 1)}]$

Updated on:21/07/2023

|

Class 12 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

A $\frac{(γ - 1) (2 ln 2 - 1)}{1 + (γ - 1) 2 ln 2}$
B $\frac{(γ - 1) (1 - 2 ln 2)}{(γ - 1) 2 ln 2 - 1}$
C $\frac{(2 ln 2 + 1) (γ - 1)}{(γ - 1) 2 ln 2 + 1}$
D $\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$
The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

A $\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$
B $\frac{(1 - 2 ln 2)}{γ / (γ - 1)}$
C $\frac{(2 ln 2 + 1)}{γ / (γ - 1)}$
D $\frac{(2 ln 2 - 1)}{γ / (γ + 1)}$

DISHA PUBLICATION-THERMODYNAMICS -EXERCISE -2 : CONCEPT APPLICATOR

Home
Ask Doubt
Profile