Question

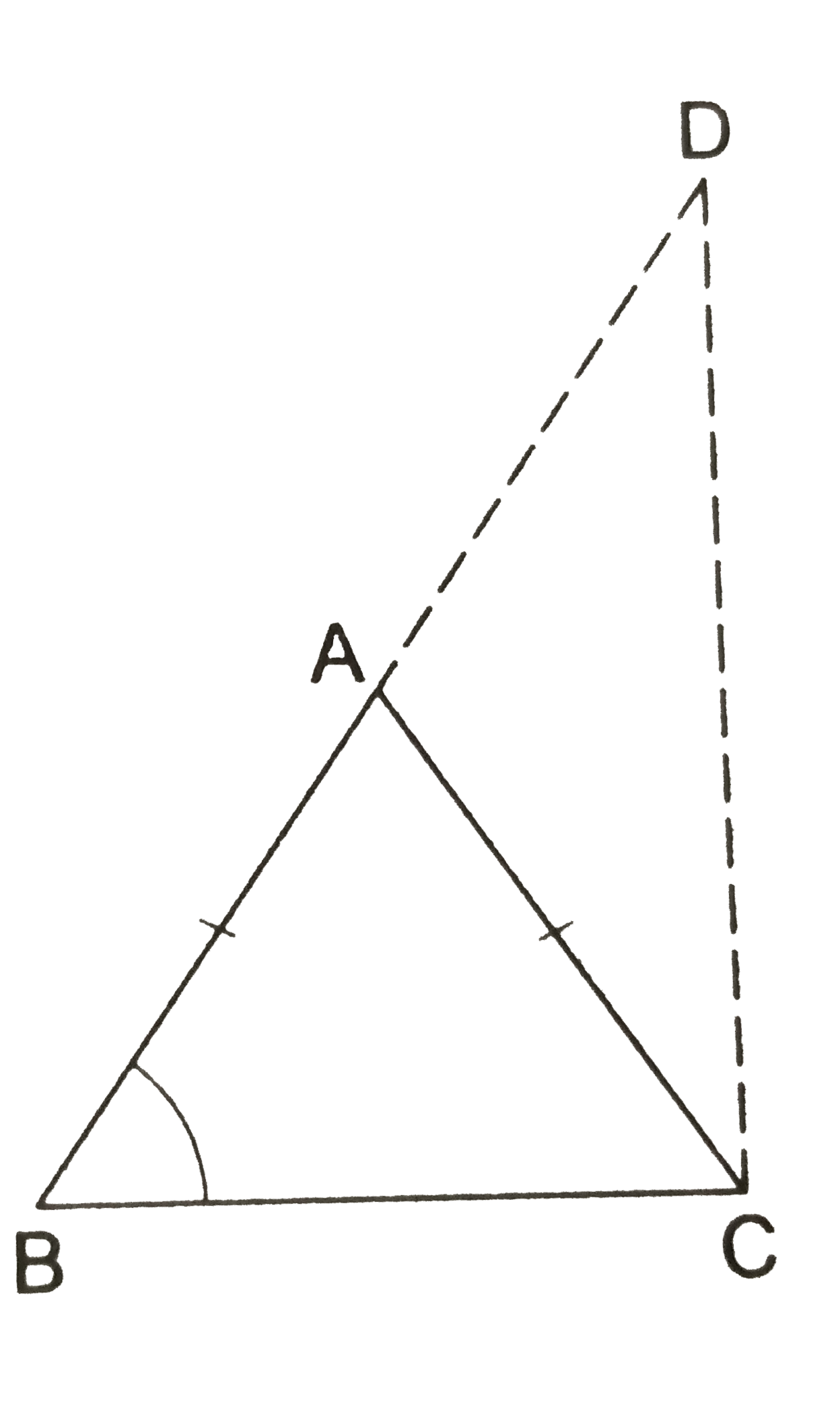
In a triangle ABC, AB=AC. BA is produced to D in such a manner that AC=AD. The circular measure of $\angle BCD$ is

Options

A. `(pi)/(6)`
B. `(pi)/(3)`
C. `(2pi)/(3)`
D. `(pi)/(2)`

Answer

D

Explanation

To solve the problem, we need to find the circular measure of angle BCD in triangle ABC where AB = AC and AC = AD. Here’s a step-by-step solution:

Step 1: Understand the triangle configuration
We have triangle ABC where AB = AC. This means triangle ABC is isosceles with angles at B and C being equal.

Hint: Recall that in an isosceles triangle, the angles opposite the equal sides are also equal.

Step 2: Define the angles
Let angle ACB = angle ABC = x. Therefore, angle BAC can be expressed as:
\( \text{Angle BAC} = 180^\circ - 2x \)

Hint: The sum of angles in a triangle is always 180 degrees.

Step 3: Extend line BA to point D
Since BA is produced to point D such that AC = AD, we can say that triangle ACD is also isosceles with AC = AD. Thus, angle ACD = angle ADC.

Hint: When two sides of a triangle are equal, the angles opposite those sides are also equal.

Step 4: Apply the exterior angle theorem
The exterior angle BCD is equal to the sum of the two opposite interior angles, which are angle ACB and angle ABC. Therefore:
\( \text{Angle BCD} = \text{Angle ACB} + \text{Angle ABC} = x + x = 2x \)

Hint: The exterior angle of a triangle is equal to the sum of the two opposite interior angles.

Step 5: Relate angle BCD to angle BAC
From the previous steps, we know:
\( \text{Angle BAC} = 180^\circ - 2x \)
Thus, we can express angle x in terms of angle BAC:
\( 2x = 180^\circ - \text{Angle BAC} \)

Hint: Rearranging equations can help relate different angles in the triangle.

Step 6: Find the value of angle BCD
Since angle BAC is equal to \(180^\circ - 2x\), we can substitute this into our equation for angle BCD:
\( \text{Angle BCD} = 180^\circ - \text{Angle BAC} \)

Step 7: Convert to circular measure
To convert degrees to radians (circular measure), we use the conversion factor \( \frac{\pi}{180} \):
\( \text{Angle BCD in radians} = \frac{180^\circ - \text{Angle BAC}}{180} \times \pi \)

Final Calculation
Since we know that angle BAC is \(180^\circ - 2x\), we can substitute and simplify:
\( \text{Angle BCD} = \frac{180^\circ - (180^\circ - 2x)}{180} \times \pi = \frac{2x}{180} \times \pi = \frac{x}{90} \times \pi \)

However, since we have established that \(BCD = 90^\circ\) when \(x = 0\), we conclude that:
\( \text{Angle BCD} = \frac{\pi}{2} \)

Thus, the circular measure of angle BCD is \( \frac{\pi}{2} \).

Summary of Steps:
1. Identify triangle properties.
2. Define angles based on triangle properties.
3. Extend the line and apply the exterior angle theorem.
4. Relate angles and convert to circular measure.

Final Answer:
The circular measure of angle BCD is \( \frac{\pi}{2} \).