Two coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
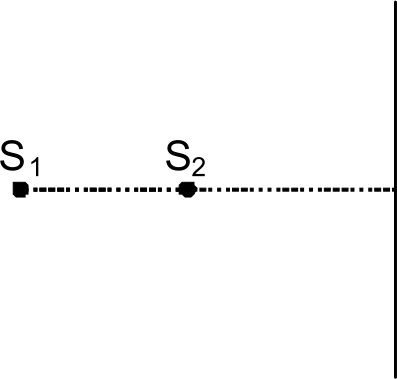
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
A dark spot will be formed at the point P2
At P2 the order of the fringe will be maximum
The total number of fringes produced between P1andPS in the first quadrant is close to 3000
The angular separation between two consecutive bright spots decreases as we move from P1toP2 along the first quadrant
The correct Answer is:B, C
Step by step video & image solution for Two coherent monochromatic point sources S_1 and S_2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero. Initially S_(1)S_(2)=2.5 lambda and the number of bright circular rings on the screen in n_(1). if the distance S_(1)S_(2) is increased and made 5.7 lambda, the number of bright circular rings becomes n_(2). the difference n_(2)-n_(1) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Part I : PHYSICS (Section 3)Paragraph 2
2 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION 1
6 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION 3)
2 Videos
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
Similar Questions
One twirls a circular ring (of mass and radius ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is ?. The finger rotates with an angular velocity 20. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is μ and the acceleration due to gravity is g.

The minimum vlaue of ω0 below which the ring will drop down is
View SolutionThe potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
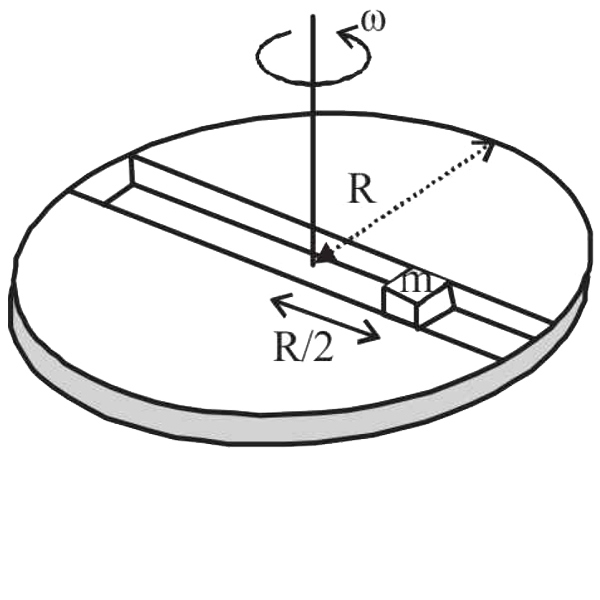
The distance r of the block at time is
View SolutionA spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
View SolutionPut a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda . The separation between the sources is 2lambda . Consider a line passing through S_(1) and perpendicular to line S_(1) S_(2) . Find the position of farthest and nearest minima. .
View SolutionTwo monochromatic coherent point sources S_(1) and S_(2) are separated by a distance L. Each sources emits light of wavelength lambda , where L gt gt lambda . The line S_(1) S_(2) when extended meets a screen perpendicular to it at point A. Then
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.

Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionRatio waves originating from sources S_(1) and S_(2) having zero phase difference and common wavelength lambda will show completely destructive interference at a point P is S_(1)P-S_(2)P is
View SolutionThree coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

View SolutionTwo sources wave S_(1) and S_(2) having zero phase difference coming from an isolated light source produces interference. If the common wavelength of the two source be lambda then it is observed that a destructive interference has been taken place at point P. The value of (S_(2)P-S_(1) P) is
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda .The separation between the sources is 2 lambda .The smallest distance from S_(2) on a line passing through S_(2) and perpendicular to S_(1)S_(2) where a minimum intensity occurs is :
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance >. Each source emits light of wavelength λ where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Which of the following is correct ?
View SolutionTwo coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View Solution
