Triangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)Solution in Tamil
Step by step video & image solution for Triangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (DeltaABC) = 1/2 ar(|| gm ABEF) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS BOOK - NCERT TAMILCHAPTER - AREAS EXERCISE - THINK, DISCUSS AND WRITE
3 Videos
- AREAS BOOK - NCERT TAMILCHAPTER - AREAS EXERCISE - EXERCISE 11.1
4 Videos
- ALGEBRABOOK - NCERT TAMILCHAPTER - ALGEBRAEXERCISE - Exercise 3.15 (Multiple choice questions)
29 Videos
- CIRCLESBOOK - NCERT TAMILCHAPTER - CIRCLESEXERCISE - EXERCISE 12.5
5 Videos
Similar Questions
If 1cm represents 5m, what would be an area of 6 square cm. represent ?
View SolutionIn ΔABC,∠ABC=90∘,AD=DC,AB=12cmandBC=6.5 cm. Find the area of ΔADB .

View SolutionIf x3+6x2+kx+6 is exactly divisible by (x+2), then k=?
View SolutionFind the values of x and y in the figures given below

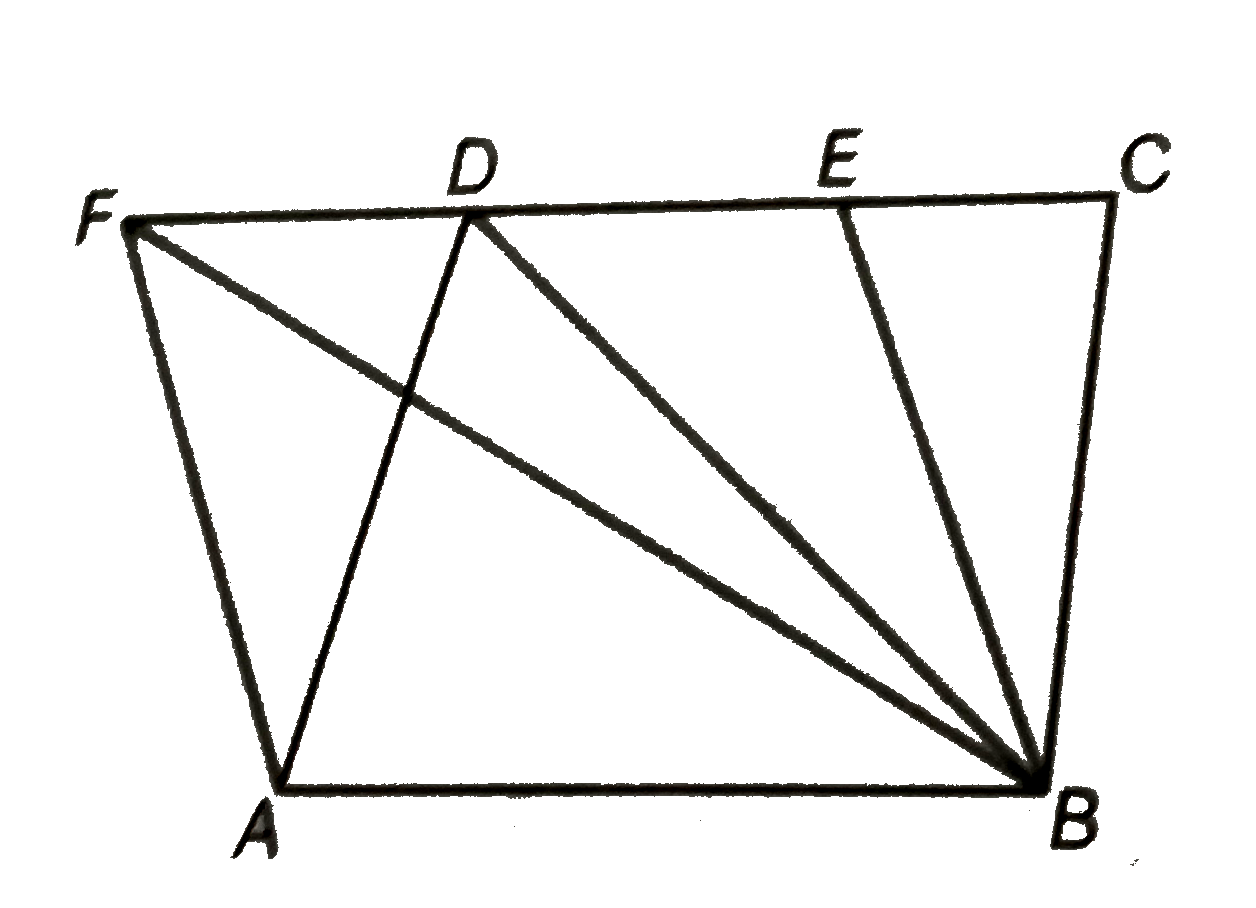
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
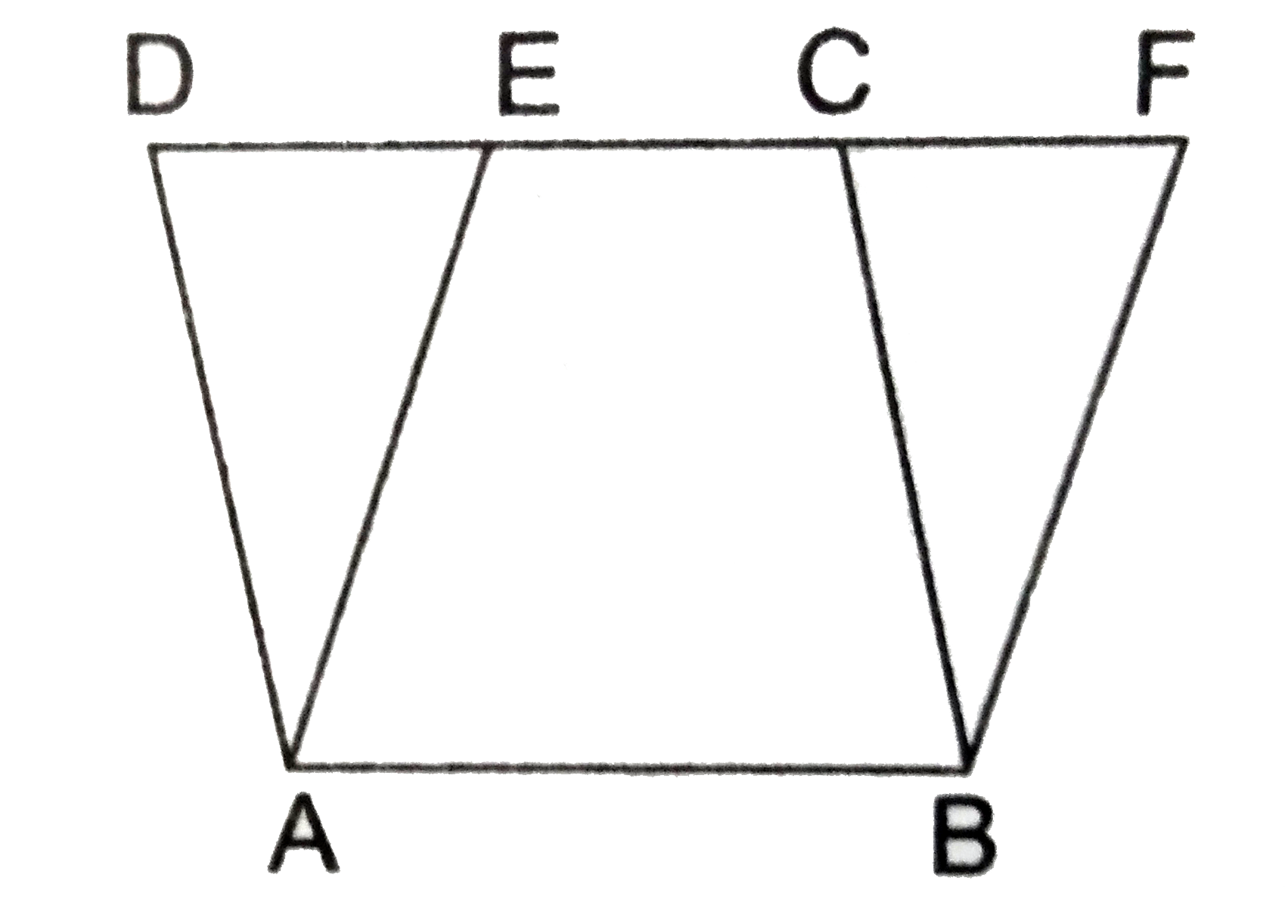
View SolutionIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
View Solutionत्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionTriangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionTriangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)
View SolutionTriangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View Solution
