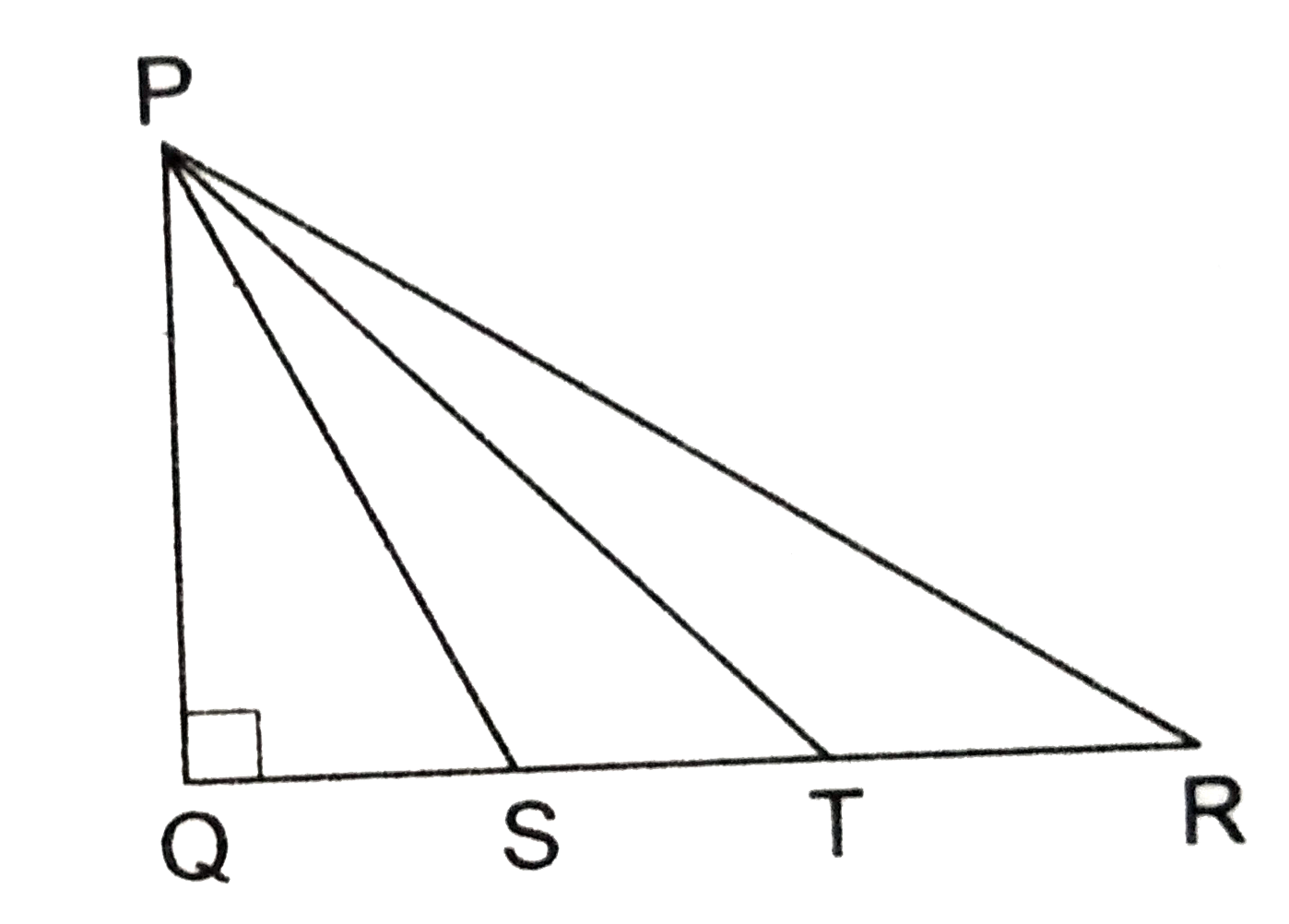
In the figure given below, $Δ P Q R$ is right-angled at Q and the points S and T trisect the side QR. Prove that $8 P T^{2} = 3 P R^{2} + 5 P S^{2}$

Video Solution

Text Solution

Verified by Experts

GIVEN $A Δ P Q R$ in which $∠ P Q R = 90^{\circ}$ , S and T are the points of trisection of QR.
TO PROVE $8 T P^{2} = 3 P R^{2} + 5 P S^{2}$
PROOF Let $A Q = S T = T R = x$ . Then,
$Q S = x, Q T = 2 x and Q R = 3 x$ .
From right triangle $P Q S, P Q T and P Q R$ by Pythagora's theorem we have,

$P S^{2} = P Q^{2} + Q S^{2}, P T^{2} = P Q^{2} + Q T^{2} and P R^{2} = P Q^{2} + Q R^{2}$
$∴ 3 P R^{2} + 5 P S^{2} - T P^{2}$
$= 3 (P Q^{2} + Q R^{2}) + 5 (P Q^{2} + Q S^{2}) - 8 (P Q^{2} - Q T^{2})$
$= 3 Q R^{2} + 5 Q S^{2} - 8 Q T^{2}$ ltbr $= 3 \times {(3 x)}^{2} + 5 {(x)}^{2} - 8 \times {(2 x)}^{2} [∴ Q R = 3 x, Q S = x and Q T = 2 x]$
$= (27 x + 5 x^{2} - x^{2}) = 0$
Thus, $3 P R^{2} + 5 P S^{2} - 8 P T^{2} = 0$
Hence, $8 P T^{2} = 3 P R^{2} = 3 P R^{2} + 5 P S^{2}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-TRIANGLES-Test Yourself

Home
Ask Doubt
Profile