In an isosceles ΔABC, the base AB is produced both wasys in P and Q such that AP×BQ=AC2
Prove that ΔACP~ΔBCQ.

CA=CB⇒∠CAB=∠CBA
⇒180∘−∠CAB=180∘−∠CBA
⇒∠CAP=∠CBQ.
Now, AP×BQ=AC2⇒APAC=ACBQ
⇒APAC=BCBQ[∴AC=BC]
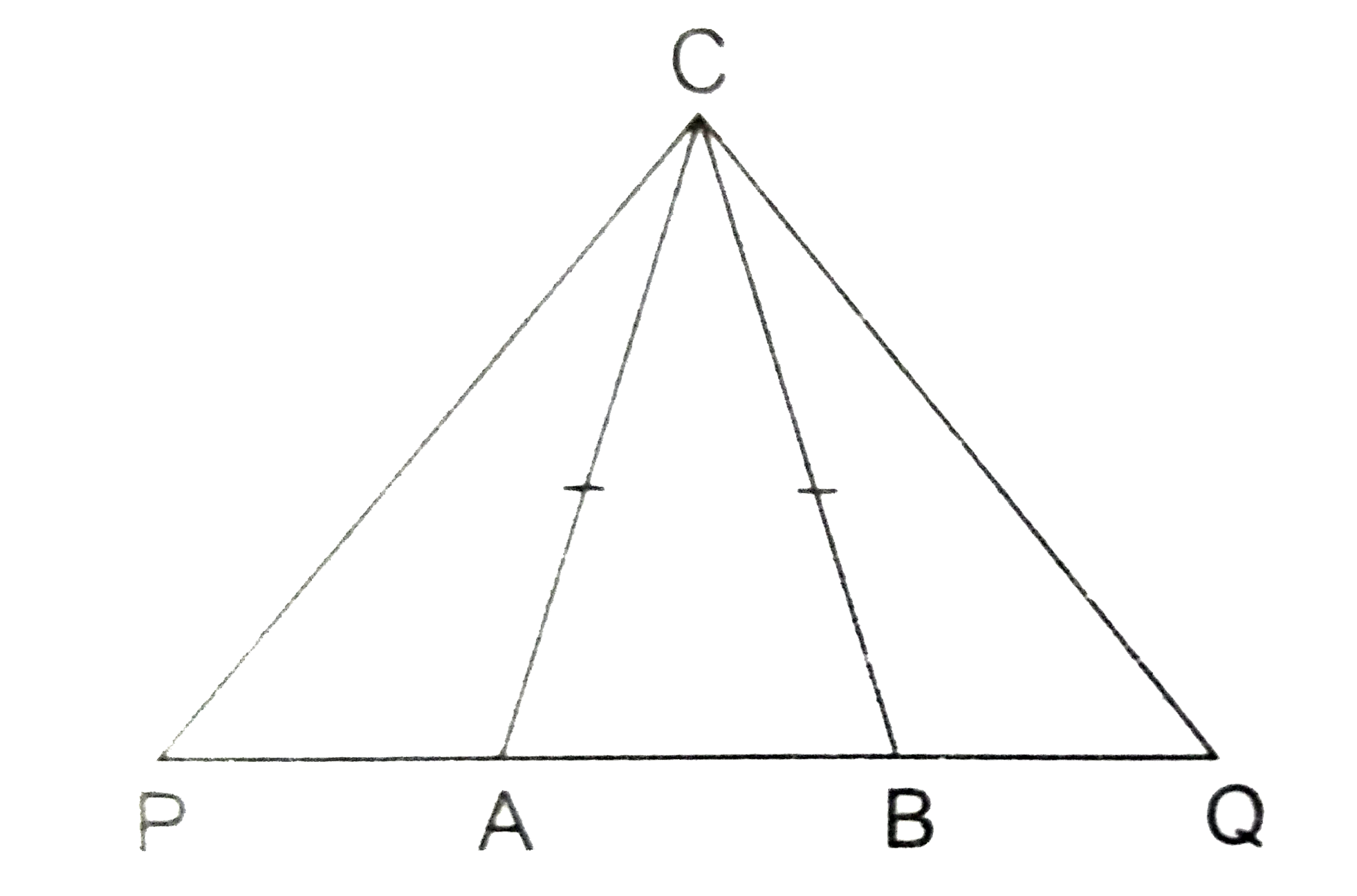
Thus, ∠CAP=∠CBQandAPAC=BCBQ
∴ΔACP~ΔBCQ.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D22videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A12videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
A30∘B45∘C60∘D90∘ - Question 2 - Select One
ΔABC,AB=AC and BA is produced to D such that AC = AD. Then the ∠BCD is
A100∘B60∘C80∘D90∘
abc is an isosceles triangle with AB=AC. Side BAis produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
 View Solution
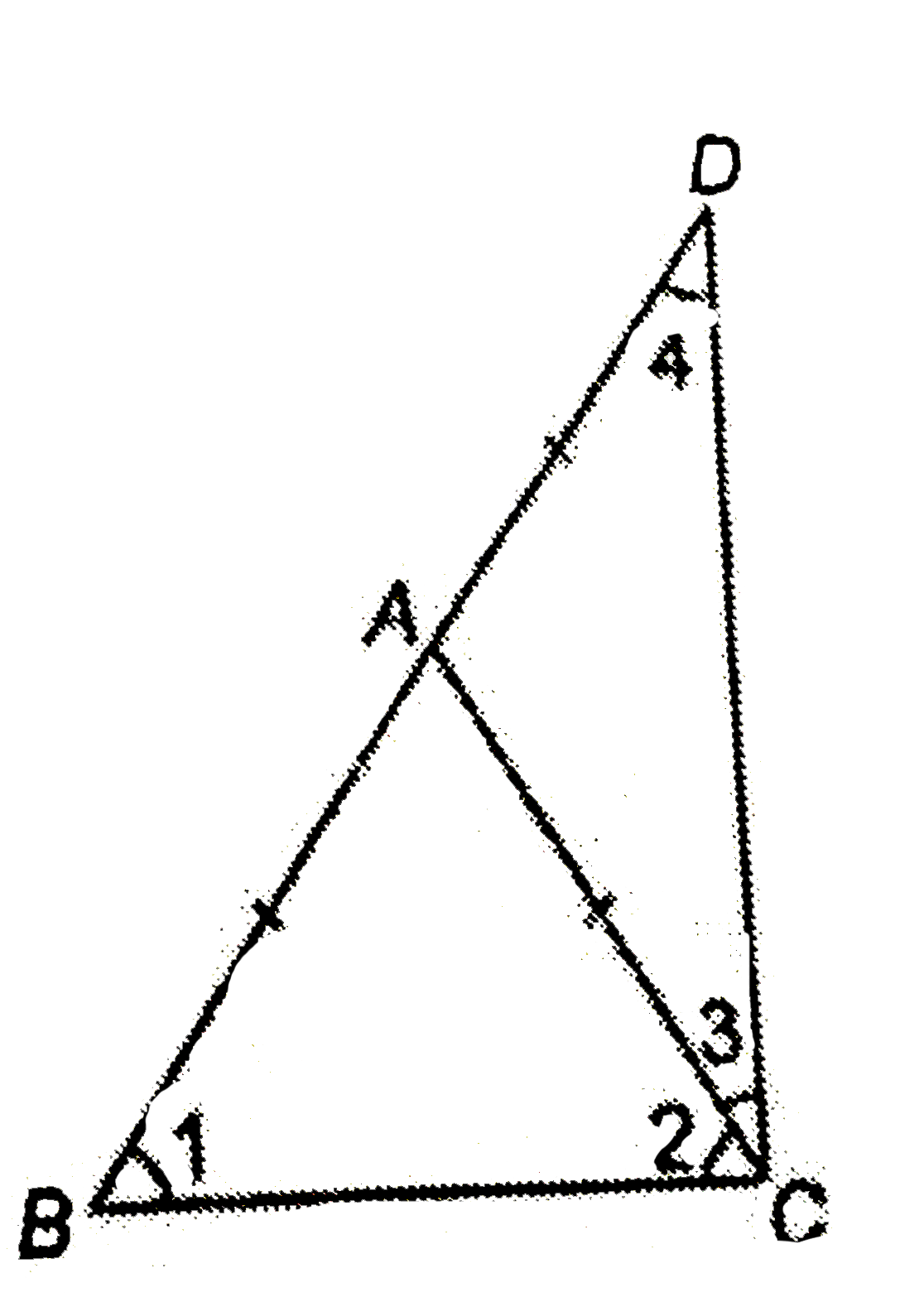
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
 View Solution
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIn the given figure, E is a point on side CB produced of an isosceles ΔABC with AB=AC.. If AD⊥BCandEF⊥AC, prove tha ΔABD~ΔECF
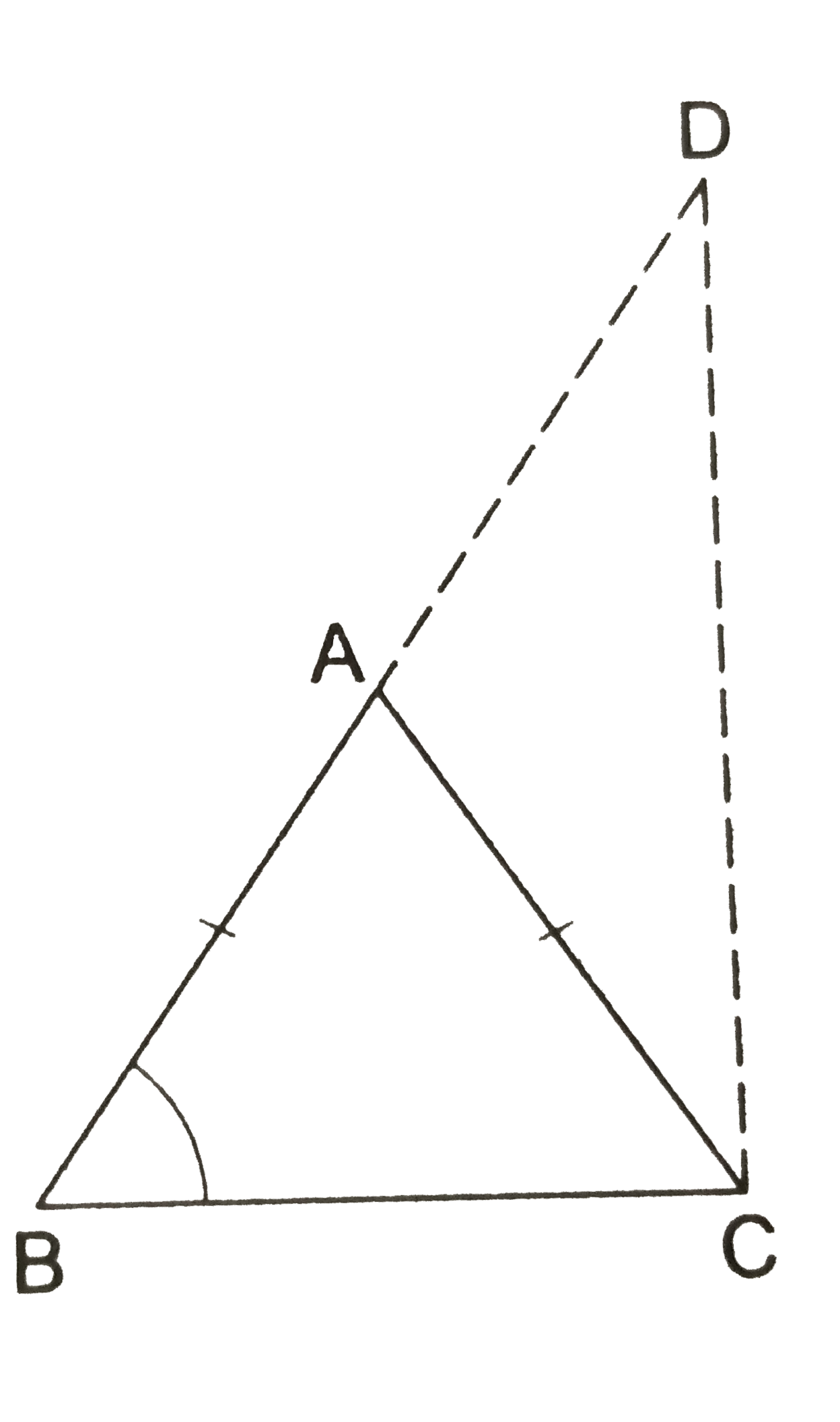
View SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
 View Solution
View Solution

