Show that the superposition of the waves originating from two coherent sources s1ands2 having displacement y1=acosωtandy2=acos(ωt+ϕ) at a point produce a result intensity IR=4a2cos2ϕ2. Hence, write the conditions for the appearance of dark and bright fringes.
If two waves are being represented as:
y1=acosωtandy2=acos(ωt+θ), then the displacement of resultant wave formed the to their superposition is given by
y=y1+y2=acosωt+acos(ωt+ϕ)=2acos(ϕ2).cos(ωt+ϕ2)
Obviously the amplitude of the resultant wave is A=2acos(ϕ2) and therefore the resultant
intensity at a point will be given by IR=kA2=k.4a2cos2(ϕ2)
But ka2=I=Intensity of light due to any one superposing wave. so, we have IR=4Icos2(ϕ2).
Condition for bright: If θ=2nπ (where n=0,1,2,3. . ), then
IR=4Icos2(nπ)=4I=maximum and we obtain bright fringe.
Condition for dark fringes: If ϕ=(2n−1)π (where n=1,2,3. . ), then
IR=4πcos2(2n−12π)=0 and we obtain dark fringe.
Topper's Solved these Questions
- WAVE OPTICSBOOK - U-LIKE SERIESCHAPTER - WAVE OPTICSEXERCISE - LONG ANSWER QUESTIONS-I
31 Videos
- WAVE OPTICSBOOK - U-LIKE SERIESCHAPTER - WAVE OPTICSEXERCISE - LONG ANSWER QUESTIONS-II
12 Videos
- WAVE OPTICSBOOK - U-LIKE SERIESCHAPTER - WAVE OPTICSEXERCISE - VERY SHORT ANSWER QUESTIONS
31 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - U-LIKE SERIESCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - SECTION B
1 Videos
Similar Questions
Knowledge Check
The displacement of two coherent light waves are given by y1=a1cosωtandy2=a2cos(π/2−ωt). The resultant intensity is given by
Aa1−a2Ba1+a2C(a21+a22)D(a21−a22)
In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:A4I0BI0C2I0DzeroIn the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be
 A4l0Bl0C2l0Dzero
A4l0Bl0C2l0Dzero
(a) (i) 'Two independent monochromatic sources light cannot produce a sustained interference pattern.' Give reasons.
(ii) Light waves each of amplitude "a" and freuency "ω", emanating from two coherent light sources superpose at a point. If the displacement due to these waves is given by y1=acosωtandy2=acos(ωt+ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double-slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View SolutionTwo waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
View SolutionTwo waves of equation
y1=acos(ωt+kx)andy2=acos(ωt−kx) are superimposed upon each other. They will produce
View Solution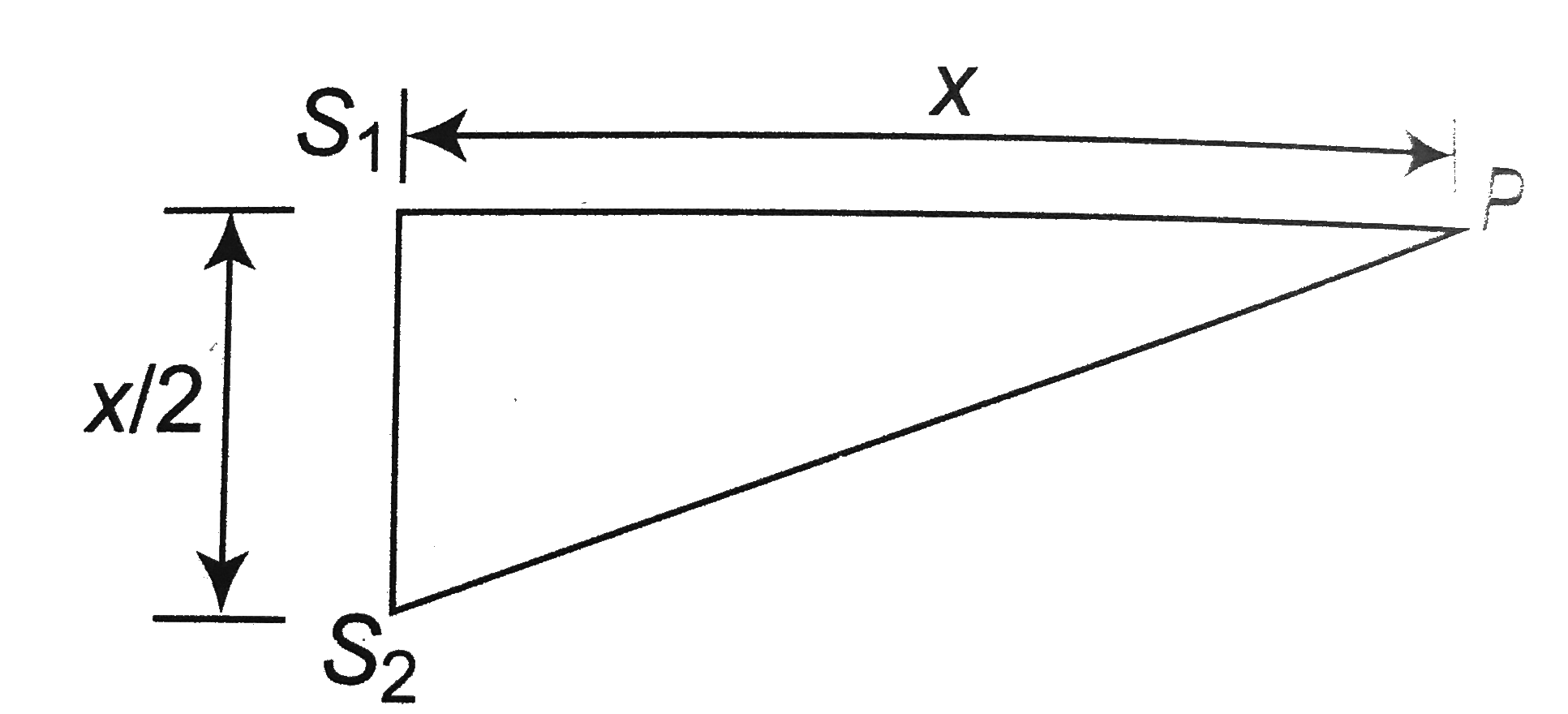
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2P
View SolutionTwo waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
View Solution
