Prove that the points A(2, 4), B(2, 6) and C(2 + √3, 5) are the vertices of an equilateral triangle.
6
5
−3
1
The correct Answer is:B
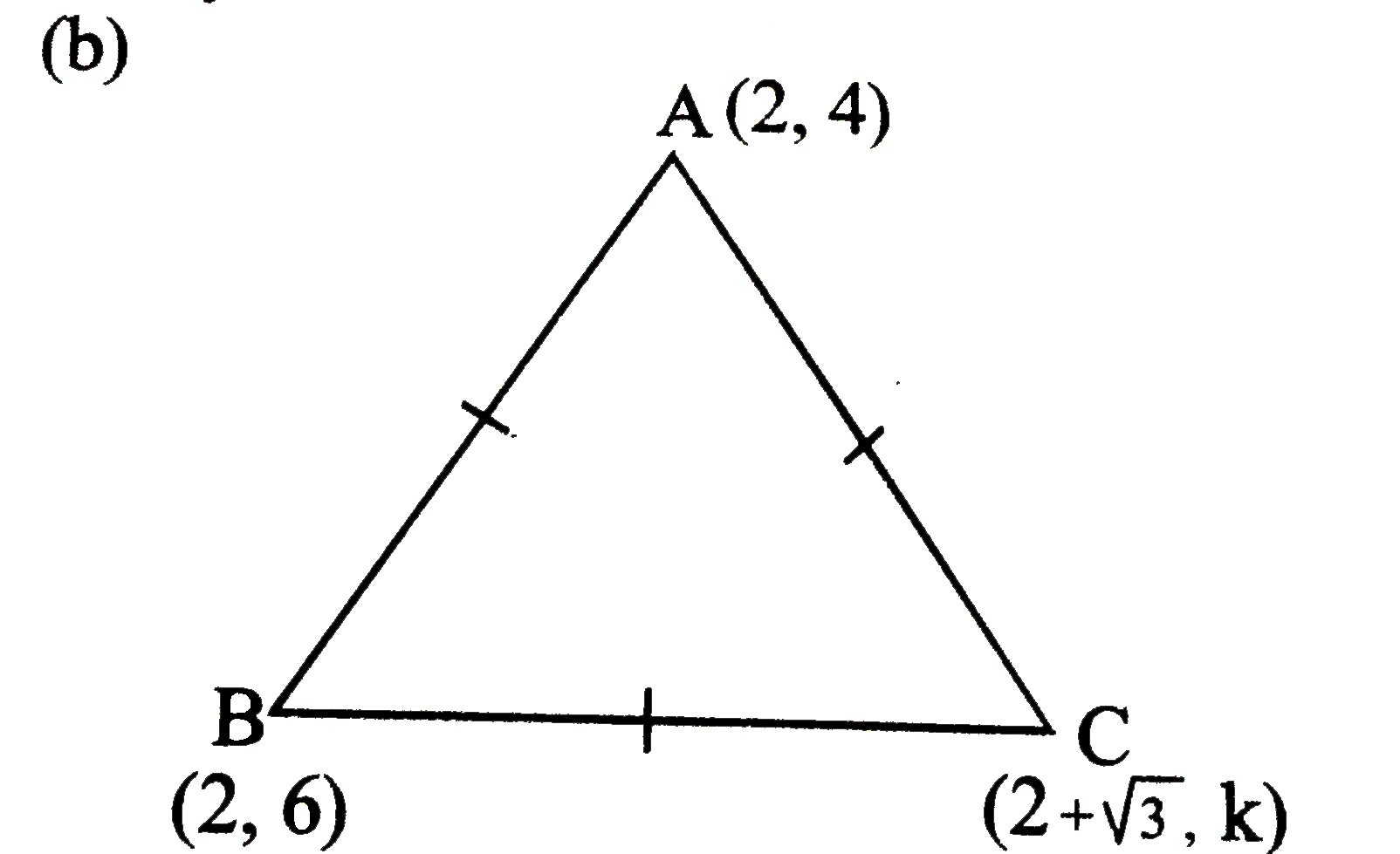
since, ABC is an equilateral Δ,
∴AB=BC=CA
Consider BC=AC
⇒√3+(k−6)2=√3+(k−4)2
⇒√39+k2−12k=√k2−8k+19
⇒k2−12k+39=k2−8k+19
⇒−4k=−20
k=5
Topper's Solved these Questions
Similar Questions
Prove that the points (2a,4a),(2a,6a)and(2a+√3a,5a) are the vertices of an equilateral triangle.
View SolutionProve that the points (2a,4a),(2a,6a)and(2a+√3a,5a) are the vertices of an equilaterall triangle whose side is 2a
View SolutionProve that the points (a,a),(−a,−a)and(−a√3,a√3) are the vertices of an equilateral triangle.
View SolutionShow that the points A(1,2),B(1,6), C(1+2√3,4) are the
vertices of an equilateral triangle .
View SolutionShow that the points A(1, 1), B(-1, -1) and C(−√3,√3) are the vertices of an equilateral triangle each of whose sides is 2√2 units.
View SolutionShow that the points (-3, -3), (3, 3) and (−3√3,3√3) are the vertices of an equilateral triangle.
View SolutionShow that the points O(0, 0), A(3,√3)and B(3,−√3) are the vertices of an equilateral triangle. Find the area of this triangle.
View SolutionProve that the points (0,0),(3,π2) and (3,π6) are the vertices of an equilateral triangle.
View Solutionshow that the points A(1,-1,-5), B(3,1,3) and C(9,1,-3) are the vertices of an equilateral triangle.
View SolutionShow that the points (1,-2,-3),(2,-3,-1) and (3,-1,-2) are the vertices of an equilateral triangle
View Solution
