Find the magnitude and direction of the resultant of two vectors A and B in terms of their magnitudes and angle $θ$ between them .
Solution in Bengali

Video Solution

Text Solution

Verified by Experts

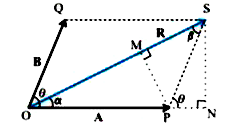
Let OP and OQ represent two vectors A and B making an angle $θ$ (Fig . 4.10) . Then , using the parallelogram method of vector addition , OS represents the resultant vector R:
R = A+B
SN is normal to OP and PM is normal to OS . From the geometry of the figure,
$O S^{2} = O N^{2} + S N^{2}$
but $O N = O P + P N = A + B cos θ$
$S N = B sin θ$
$O S^{2} = {(A + B cos θ)}^{2} + {(B sin θ)}^{2}$
or , $R^{2} = A^{2} + B^{2} + 2 A B cos θ$
$R = \sqrt{A^{2} + B^{2} + 2 A B cos θ}$
In $Δ O S N S N = O S$ sinalpha=Rsinalpha,and $< b r > \in$ DeltaPSN,SN=PSsintheta=Bsintheta $< b r > T h e r e f or e,$ R sinalpha=Bsintheta $< b r > or$ (R)/(sintheta)=(B)/(sinalpha) $< b r > s i m i l a r l y < b r >$ PM=Asinalpha=Bsinbeta $< b r > or$ (A)/(sinbeta)=(B)/(sinalpha) $< b r > or C o m b \in \in g E q s . (4.24 b) and (4.24 c), w e \geq t < b r >$ (R)/(sintheta)=(A)/(sinbeta)=(B)/(sinalpha) $< b r > U sin g E q . (424 a) . < b r > or,$ tanalpha=(SN)/(OP+PN)=(Bsintheta)/(A+Bcostheta)
Equation (4.24a) gives the magnitude of the resultant and Eqs . (4.24e) and (4.24f) its direction. Equantion (4.24a) is known as the Law of cosines and Eq . (4.24d) as the Law of sines.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

NCERT BANGLISH-MOTION IN A PLANE-EXCERCISES

Home
Ask Doubt
Profile