As per Ampere's circular law ∮→B.→dl =……………….. .
μ0∑I enclosed
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - TRUE OR FALSE
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION-REASON TYPE QUESTIONS
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - MULTIPLE CHOICE QUESTIONS
35 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
If →B1,→B2 and →B3 are the magnetic field due to l1,l2 and l3, then in Ampere's circuital law ∮→B.→dl=μ0l,→B is

View SolutionExplain how Biot-Savart's law enables one to express the Ampere's circuital law in the integral form , viz.,
∮→B.→dl=μ0I
where I is the total current passing through the surface.
View Solution
Knowledge Check
As per Ampere - Maxwell.s circuital law
A∮→B.→dl=μ0ICB∮→B.→dl=μ0(IC+ID)C∮→B×→dl=μ0(IC+ID)D∮→B×→dl=μ0IC+∈0dϕEdtIf →B1,→B2 and →B3 are the magnetic field due to l1,l2 and l3, then in Ampere's circuital law ∮→B.→dl=μ0l,→B is
 A→B=→B1−→B2B→B=→B1+→B2+→B3C→B=→B1−→B2+→B3D→B=→B3
A→B=→B1−→B2B→B=→B1+→B2+→B3C→B=→B1−→B2+→B3D→B=→B3Statement 1: →a,→band→c arwe three mutually perpendicular unit vectors and →d is a vector such that →a,→b,→cand→d are non- coplanar. If [→d→b→c]=[→d→a→b]=[→d→c→a]=1, then →d=→a+→b+→c
Statement 2: [→d→b→c]=[→d→a→b]=[→d→c→a]⇒→d is equally inclined to →a,→band→c.ABoth the statements are true and statement 2 is the correct explanation for statement 1.BBoth statements are true but statement 2 is not the correct explanation for statement 1.CStatement 1 is true and Statement 2 is falseDStatement 1 is false and Statement 2 is true.
In Ampere's law (∮(→B).(→dl))=(μ0)I, the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law , gives the contribution of only the currents crossing the area bounded by the curve?
View SolutionIn Ampere's law (∮(→B).(→dl))=(μ0)I, the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law , gives the contribution of only the currents crossing the area bounded by the curve?
View SolutionYou know that Ampere's circuital law is mathematically expressed as given below.
∮→B→dt−μ0I
Also you know that this law was corrected by Maxwell and which is known as Ampere-Maxwell law. Write the general form of the law and name the additional term.
View SolutionStatement 1: →a,→band→c arwe three mutually perpendicular unit vectors and →d is a vector such that →a,→b,→cand→d are non- coplanar. If [→d→b→c]=[→d→a→b]=[→d→c→a]=1, then →d=→a+→b+→c
Statement 2: [→d→b→c]=[→d→a→b]=[→d→c→a]⇒→d is equally inclined to →a,→band→c.
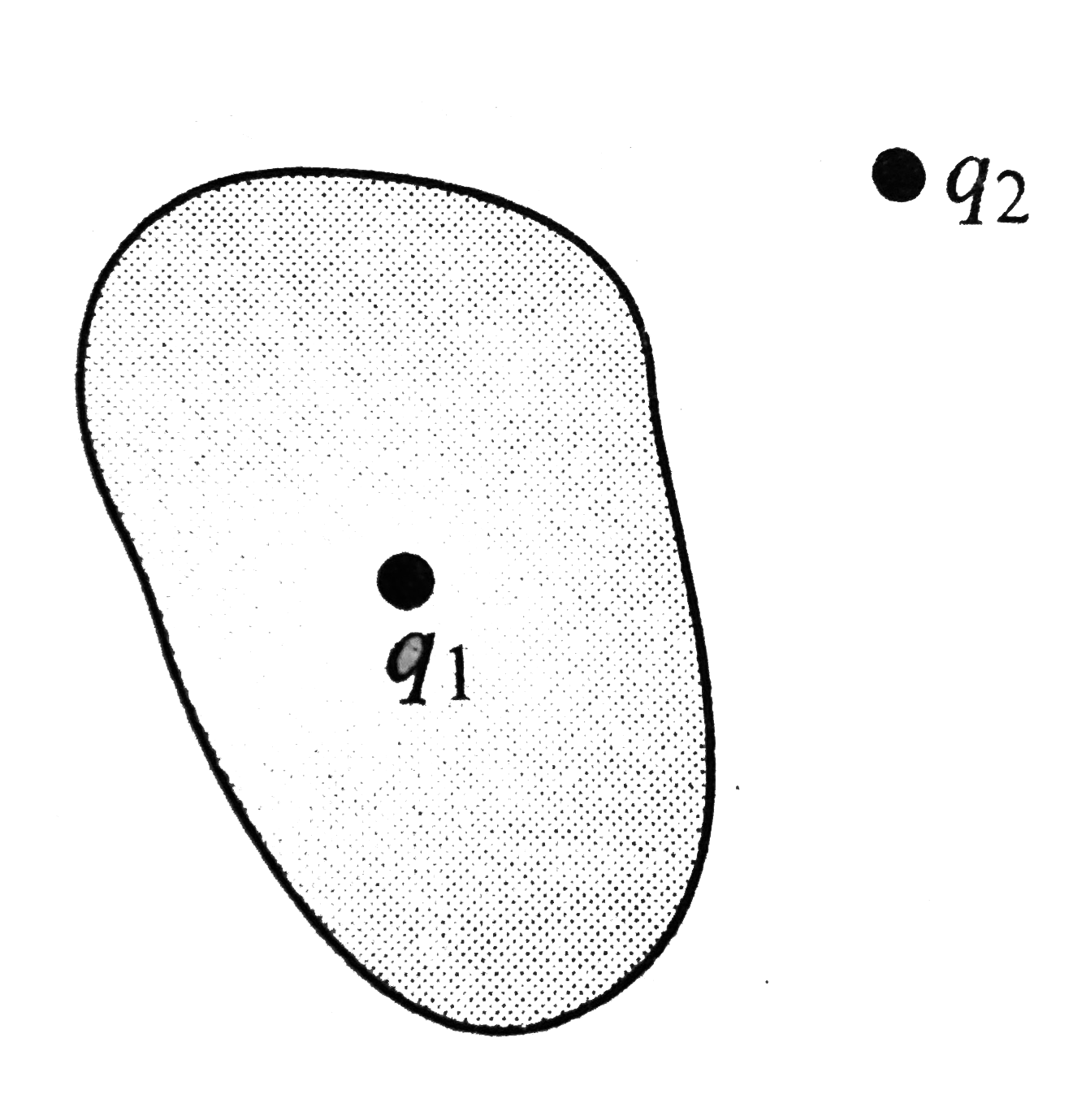
View SolutionConsider Gauss's law
∮→E⋅→ds=qε0
Then, for the situation shown in figure at the Gaussian surface
View Solution
