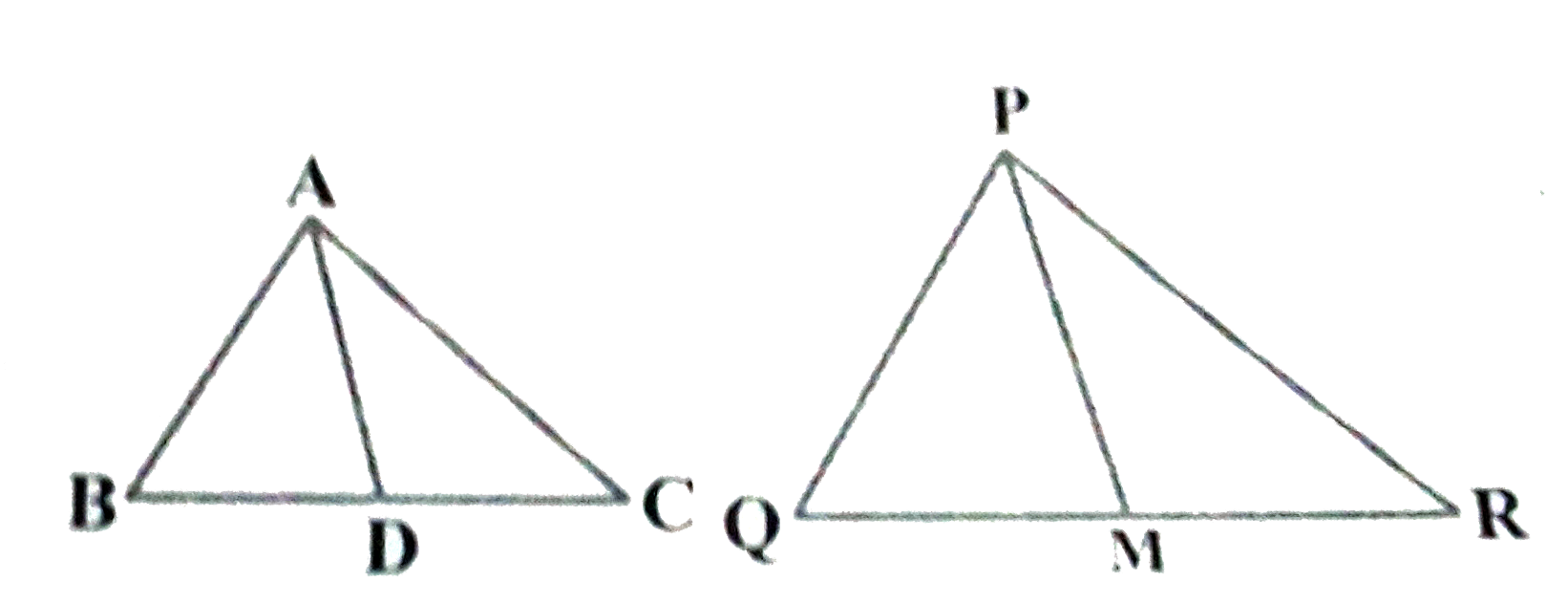
If AD and PM are medians of triangles ABC and PQR, respectively where $Δ A B C ~ Δ P Q R$ , prove that $\frac{A B}{P Q} = \frac{A D}{P M}$

Video Solution

Text Solution

Verified by Experts

from diagram
BD=DC=1/2BC and QM=MR=1/2QR
there ratio should also be same
$\frac{B D}{Q M} = \frac{B C}{Q R} = \frac{A B}{P Q} - (1)$
$∠ A B D ~ ∠ P Q M - (2)$ (SAS)
from 1 and 2
$\frac{A D}{P M} = \frac{A B}{P Q} = \frac{B P}{Q M}$

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

Similar Questions

In figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) $Δ A B C ~ Δ A M P$ (ii) $\frac{C A}{P A} = \frac{B C}{M P}$

View Solution
In figure Cm and RN are respectively the medians of $Δ A B C$ and $Δ P Q R$ . If $Δ A B C ~ Δ P Q R$ , prove that: (i) $Δ A M C ~ Δ P N R$ (ii) $\frac{C M}{R N} = \frac{A B}{P Q}$ (ii) $Δ C M B ~ Δ R N Q$
View Solution
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : $\frac{A B}{P Q} = \frac{A D}{P M}$
View Solution
In a $A B C, E a n d F$ are the mid-points of $A C a n d A B$ respectively. The altitude $A P$ to $B C$ intersects $F E$ at $Q$ . Prove that $A Q = Q P$ .
View Solution
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of $Δ P Q R$ . Show that $Δ A B C ~ Δ P Q R$ .

View Solution
In figure PS is the bisector of $∠ Q P R$ of $Δ P Q R$ . Prove that $\frac{Q S}{S R} = \frac{P Q}{P R}$ .

View Solution
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that : $\frac{A B}{P Q} = \frac{A D}{P M}$
View Solution
In Figure $P Q ∣ ∣ C D$ and $P R ∣ ∣ C B . P r o v e \frac{A Q}{Q D} = \frac{A R}{R B} .$
View Solution
In the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that $Δ A B C and Δ P Q R$ are congruent.

View Solution
In Figure, $l ∣ ∣ m$ Name three pairs of similar triangles with proper correspondence; write similarties. Prove that $\frac{A B}{P Q} = \frac{A C}{P R} = \frac{B C}{R Q}$
View Solution

Recommended Questions

Home
Ask Doubt
Profile