Observe and then find ∠P.
To find the measure of angle P in triangle RQP, we will use the properties of similar triangles and the angle sum property. Here’s a step-by-step solution:
Step 1: Identify the triangles and their sides
We have two triangles: triangle ABC and triangle RQP. The sides of triangle ABC are given as:
- AB=3.8
- BC=6
- AC=3√3
The sides of triangle RQP are given as:
- RQ=7.6
- QP=12
- PR=6√3
Step 2: Check the ratios of corresponding sides
We need to find the ratios of the corresponding sides of the two triangles to see if they are similar.
1. For AB and RQ:
ABRQ=3.87.6=3876=12
2. For BC and QP:
BCQP=612=12
3. For AC and PR:
ACPR=3√36√3=36=12
Step 3: Conclude similarity of triangles
Since all the ratios of the corresponding sides are equal:
ABRQ=BCQP=ACPR=12
By the SSS (Side-Side-Side) similarity criterion, triangle ABC is similar to triangle RQP.
Step 4: Find corresponding angles
From the similarity of triangles, we know that corresponding angles are equal. Therefore:
∠C=∠P
Step 5: Calculate angle C
Using the angle sum property in triangle ABC:
∠A+∠B+∠C=180∘
Given:
- ∠A=80∘
- ∠B=60∘
Substituting the values:
80∘+60∘+∠C=180∘
∠C=180∘−80∘−60∘=40∘
Step 6: Conclude the value of angle P
Since ∠C=∠P, we have:
∠P=40∘
Final Answer:
∠P=40∘
---
We have two triangles: triangle ABC and triangle RQP. The sides of triangle ABC are given as:
- AB=3.8
- BC=6
- AC=3√3
- RQ=7.6
- QP=12
- PR=6√3
We need to find the ratios of the corresponding sides of the two triangles to see if they are similar.
ABRQ=3.87.6=3876=12
BCQP=612=12
ACPR=3√36√3=36=12
Since all the ratios of the corresponding sides are equal:
ABRQ=BCQP=ACPR=12
By the SSS (Side-Side-Side) similarity criterion, triangle ABC is similar to triangle RQP.
From the similarity of triangles, we know that corresponding angles are equal. Therefore:
∠C=∠P
Using the angle sum property in triangle ABC:
∠A+∠B+∠C=180∘
Given:
- ∠A=80∘
- ∠B=60∘
80∘+60∘+∠C=180∘
∠C=180∘−80∘−60∘=40∘
Since ∠C=∠P, we have:
∠P=40∘
∠P=40∘
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.4
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.1
3 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.2
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
Similar Questions
The mean and variance of 5 observations are respectively 4.4 and 8.24. If three observation are 1,2 and 4 then find the remaining two observations.
View SolutionA balloon of radius r subtends an angleα at the eyes of an observer and the center of balloon from the eye is β . Find the height of the center of the balloon from the eye of observer .
View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be
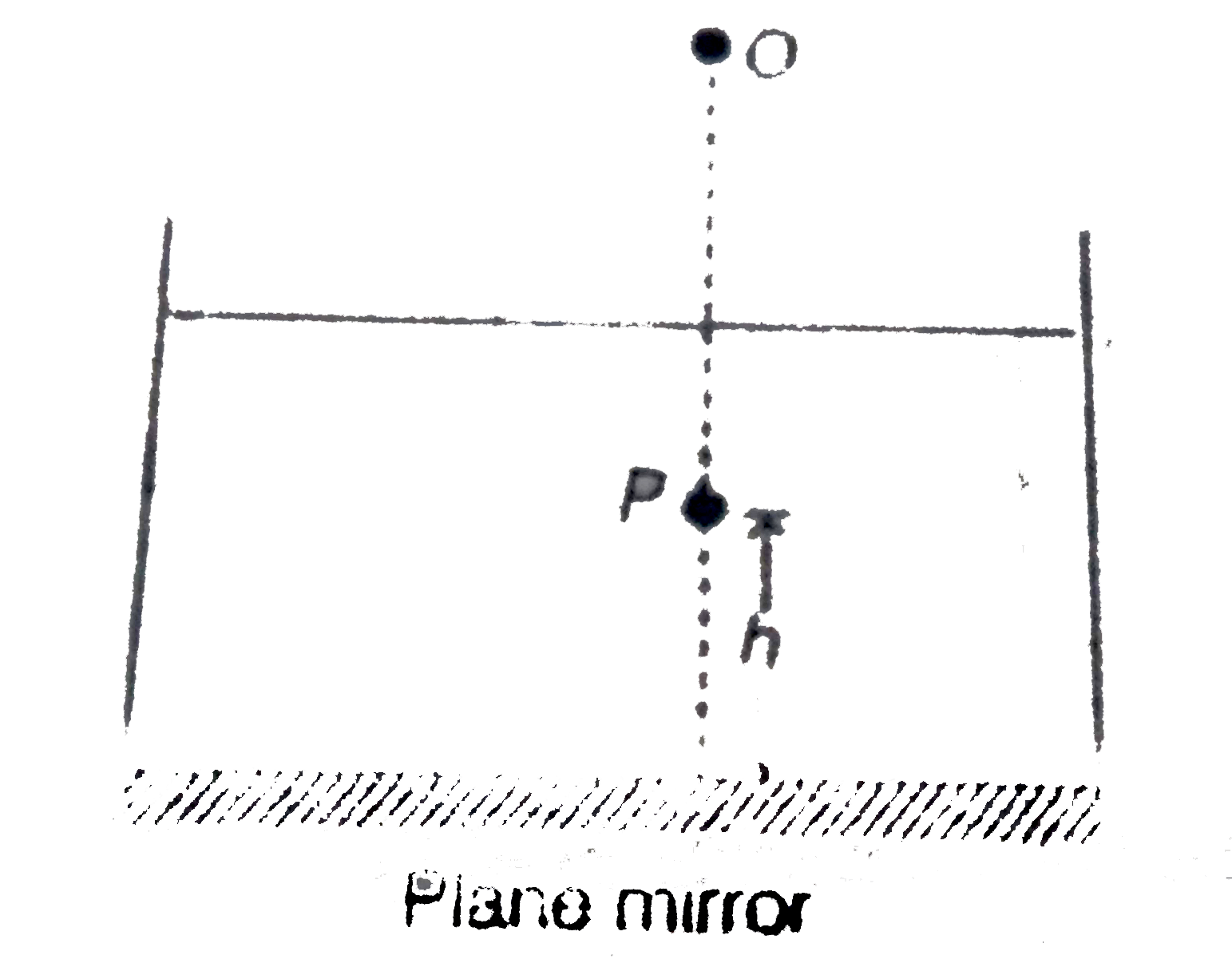
View Solution
If a polarised light of intensity l0/2 is passed through two polariods P1 and P2 as shown in figure. Then the intensity of light observed by an observer on other side of P2 (if the polaroid P1 is rotated clockwise) as a funtion of angle θ.
View SolutionFind the apparent depth of object of the object seen by observe A (in the figure shown)
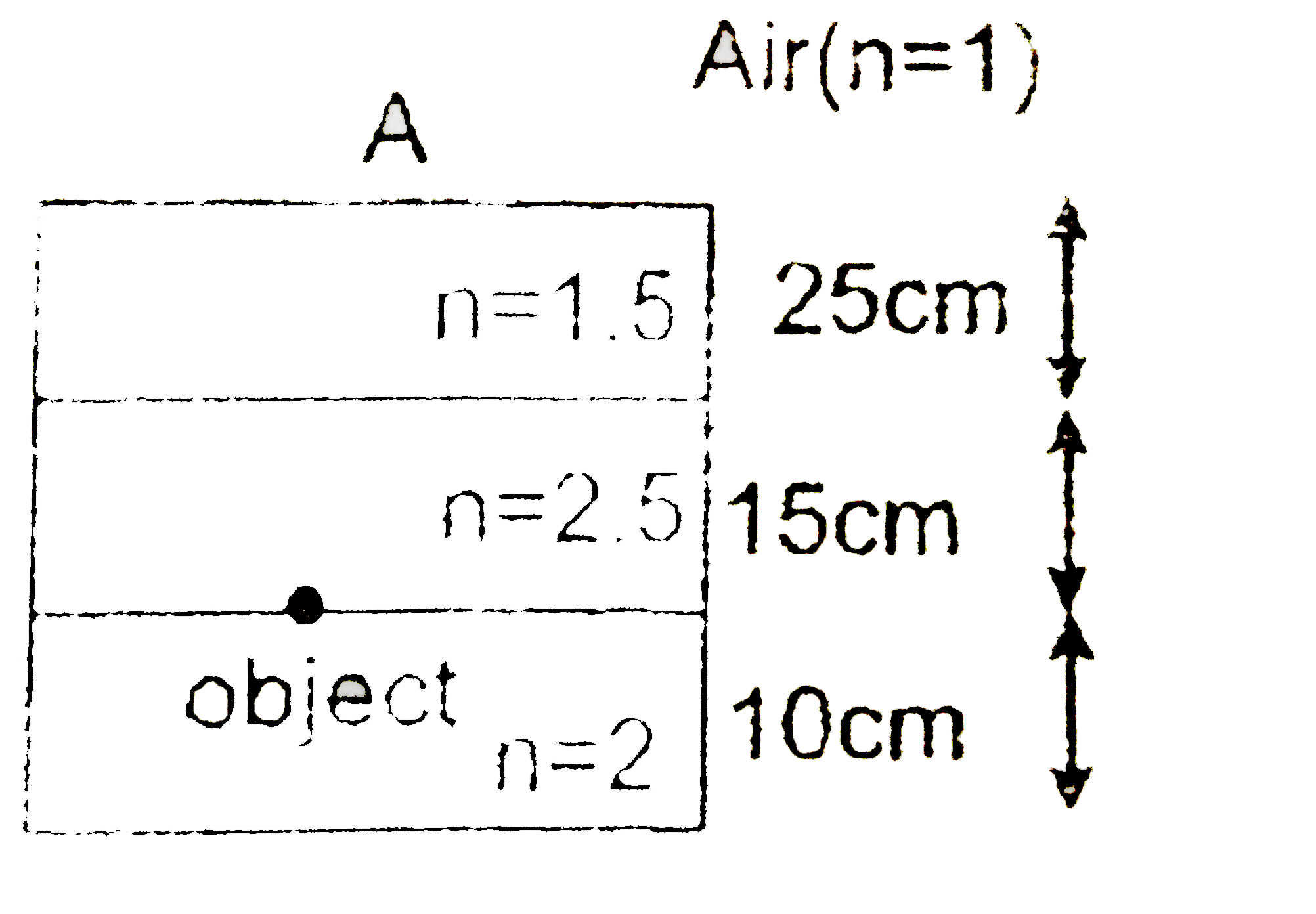
View SolutionFor a data containing 100 observations, the mean is 8. For 50 observations selected from these 100observations, the mean is 10. Find the mean of the other 50 observations.
View SolutionMean and standard deviations of 10 observations are 20 and 2 respectively. If p (p≠0) is multiplied to each observation and then q (q≠0) is subtracted then new mean and standard deviation becomes half of original value . Then find q
View SolutionObserve the following sequence of reaction and find the structure of A.
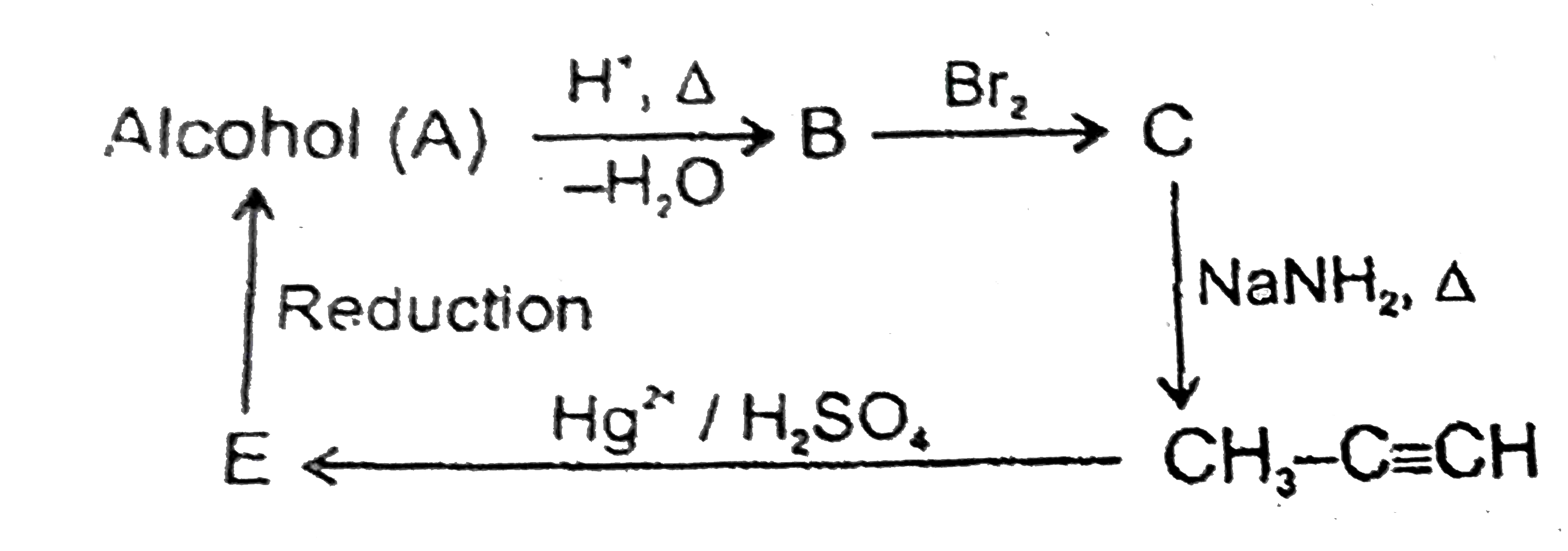
View SolutionIn a series of 2n observations, half of them equals to a and remaining half equals to -a. If the standard deviation of the observations is 2, then find |a|.
View SolutionObserve the following diagram and find the relation between compound R & S
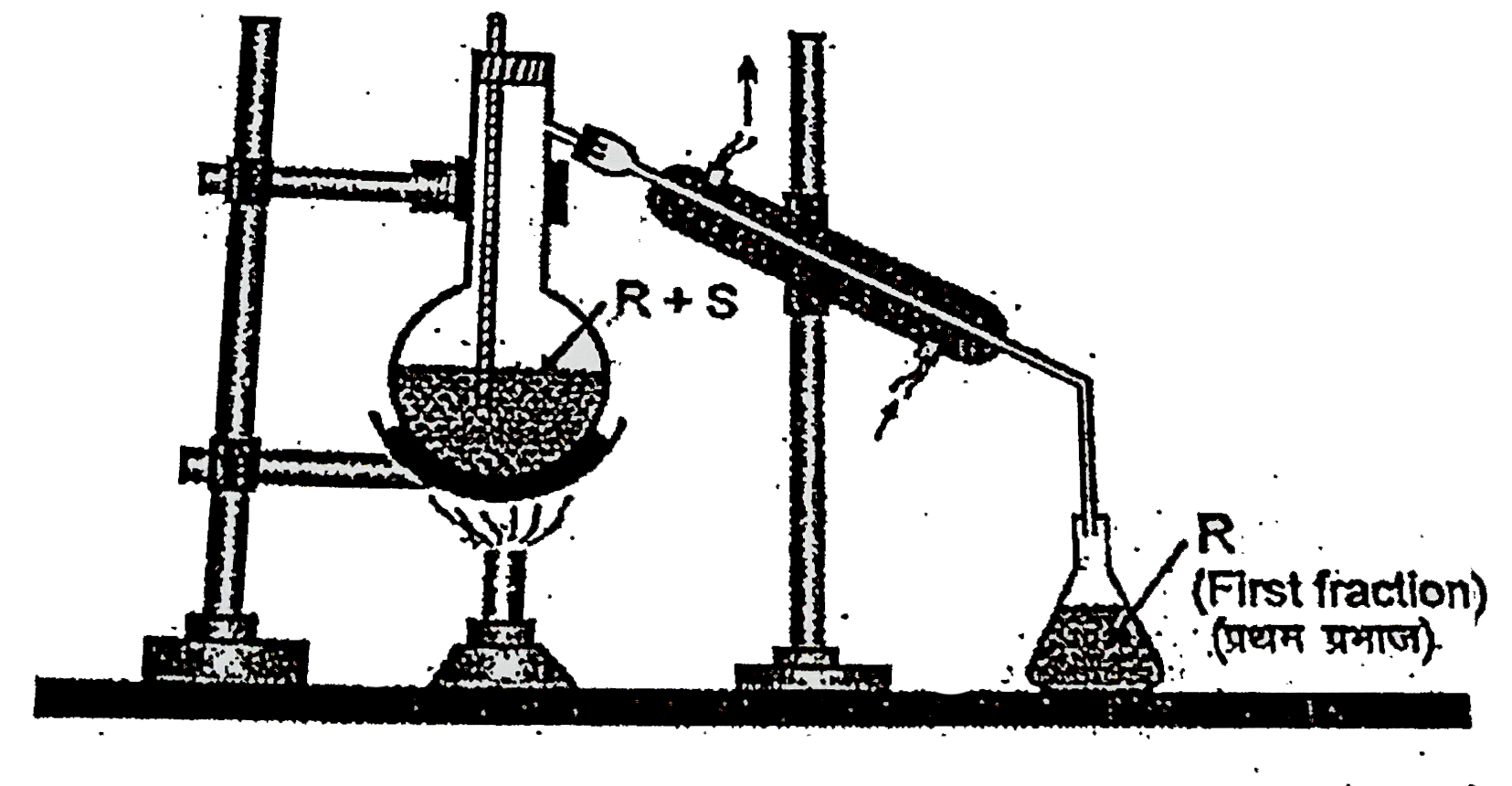
View Solution
