In two concentric circle, prove that a chord of larger circle which is tangent to smaller circle is bisected at the point of contact.
To prove that a chord of a larger circle, which is tangent to a smaller concentric circle, is bisected at the point of contact, follow these steps:
1. Understand the Setup:
- Let the center of both concentric circles be O.
- Let the radius of the smaller circle be r and the radius of the larger circle be R.
- Let AB be the chord of the larger circle that is tangent to the smaller circle at point P.
2. Draw the Diagram:
- Draw two concentric circles with center O.
- Draw the chord AB of the larger circle such that it touches the smaller circle at point P.
3. Draw the Perpendicular:
- Draw a line segment OP from the center O to the point of contact P.
- According to the property of tangents, this line OP is perpendicular to the chord AB at point P. Thus, OP⊥AB.
4. Apply the Perpendicular Bisector Theorem:
- The theorem states that if a perpendicular is drawn from the center of a circle to a chord, it bisects the chord.
- Since OP is perpendicular to AB, it bisects AB at point P.
5. Conclude the Proof:
- Therefore, we can conclude that AP=PB.
- This means that the chord AB is bisected at the point of contact P.
Final Statement:
Thus, we have proved that a chord of a larger circle, which is tangent to a smaller concentric circle, is bisected at the point of contact.
---
- Let the center of both concentric circles be O.
- Let the radius of the smaller circle be r and the radius of the larger circle be R.
- Let AB be the chord of the larger circle that is tangent to the smaller circle at point P.
- Draw two concentric circles with center O.
- Draw the chord AB of the larger circle such that it touches the smaller circle at point P.
- Draw a line segment OP from the center O to the point of contact P.
- According to the property of tangents, this line OP is perpendicular to the chord AB at point P. Thus, OP⊥AB.
- The theorem states that if a perpendicular is drawn from the center of a circle to a chord, it bisects the chord.
- Since OP is perpendicular to AB, it bisects AB at point P.
- Therefore, we can conclude that AP=PB.
- This means that the chord AB is bisected at the point of contact P.
Thus, we have proved that a chord of a larger circle, which is tangent to a smaller concentric circle, is bisected at the point of contact.
Topper's Solved these Questions
Similar Questions
Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View SolutionIn two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View SolutionIn two concentric circles, a chord of length 24cm of larger circle becomes a tangent to the smaller circle whose radius is 5cm. Find the radius of the larger circle.
View SolutionProve that all the chords of a circle through a given point within it, the least is one which is bisected at that point.
View SolutionProve that all the chords of a circle through a given point within it, the least is one which is bisected at that point.
View SolutionThe shows two concentric circles and AD is a chord of lenger circle. prove that AB=CD
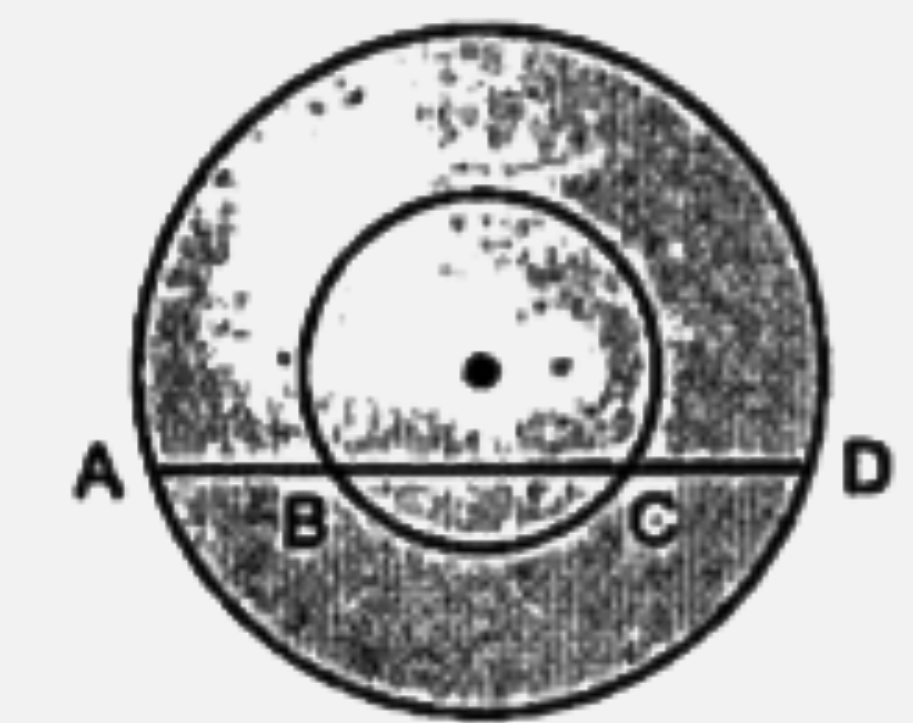
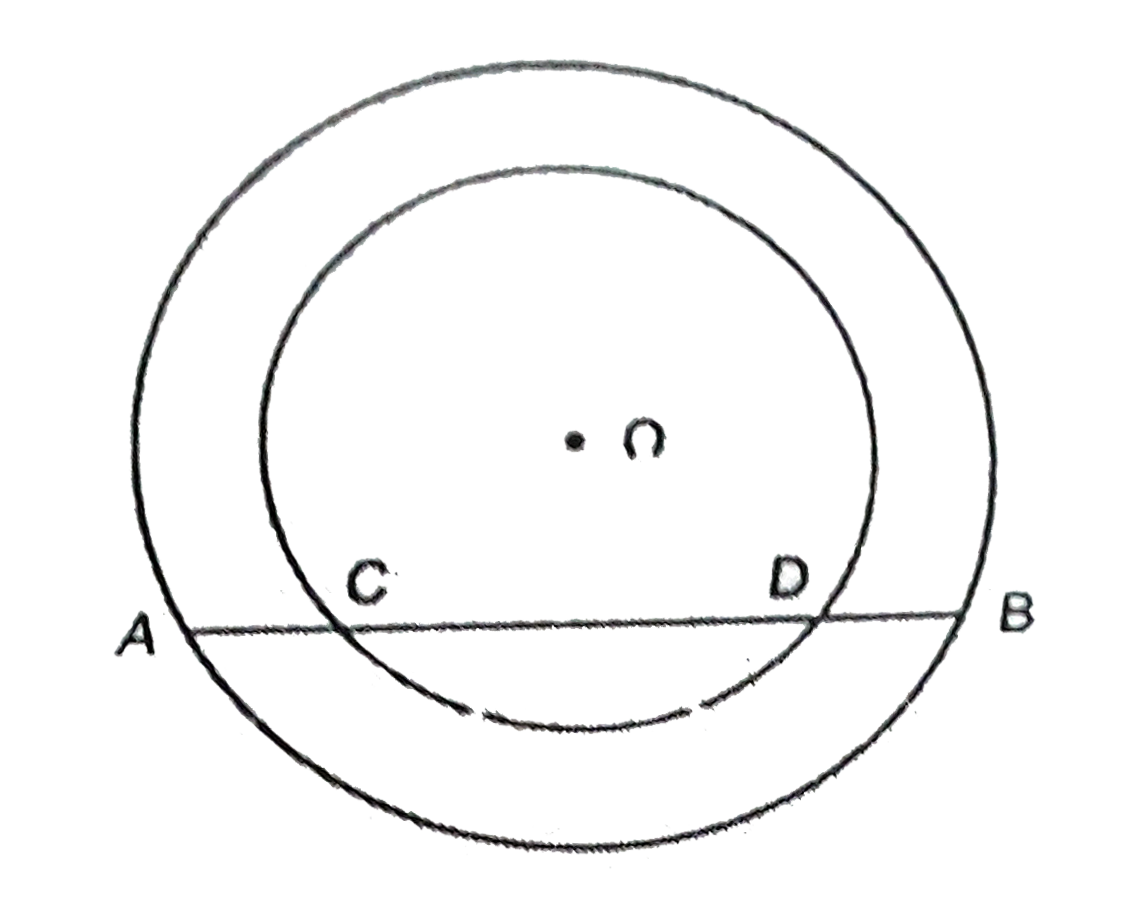
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View SolutionIf radii of two concentric circles are 4 cm and 5 cm, then length of each chord of one circle which is tangent to the other circle, is
View SolutionIf the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
View SolutionThe figure shows two concentric circles and AD is a chord of larger circle.
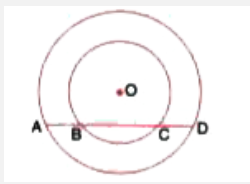
Prove that : AB = CD.
View Solution
