Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Figure). Prove that ∠ACP=∠QCD.
angles substended by arc AD on same side are equal.
∠ACP=∠ABP are QD angles subtended by arc QD on same side∠QCD=∠QBP.
Similar Questions
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View SolutionTwo congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View SolutionTwo cirlces intersect at P and Q . Through P diameter PA and PB of the two circles are drawn. Show that the points A,Q and B are collinear.
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionTwo tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120∘ . Prove that OP=2 AP .
View SolutionIf two circles touching both the axes intersect at two points P and Q where P=(3,1) then PQ=
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionTwo circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
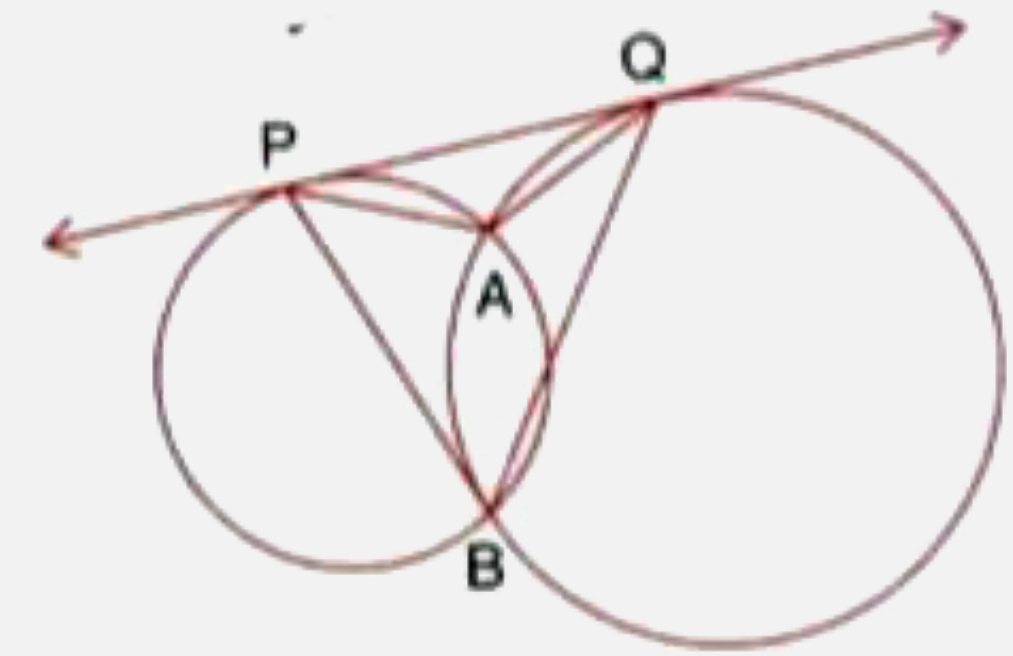
View SolutionCircles with centres P and Q intersects at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent, show that : CE = BD.
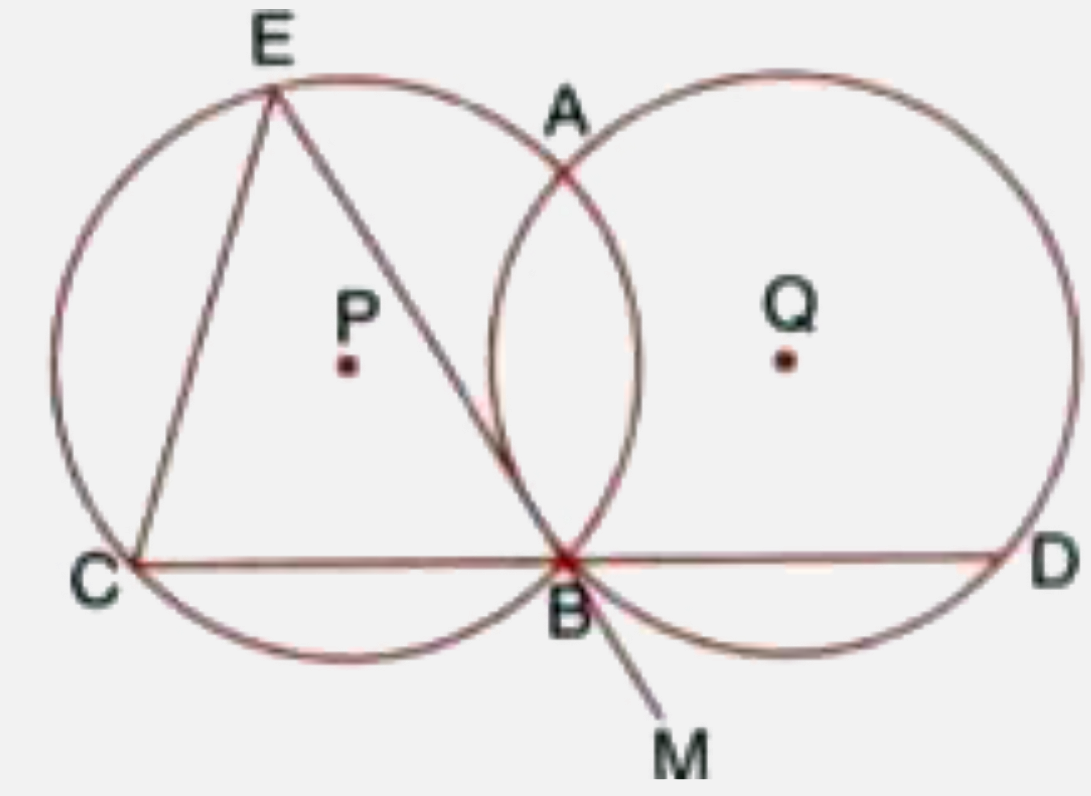
View SolutionTwo circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD=2 OO'
View Solution
