In Fig 7.31, DA⊥AB,CB⊥ABandAC=BD. State the three pairs of equal parts in ΔABCandΔDAB. Which of the following statements is meaningful? (i) ΔABC[_≅?]ΔBAD (ii) ΔABC[_≅?]ABD
To solve the problem, we need to identify the three pairs of equal parts in triangles ABC and DAB, and then determine which of the given statements about the congruence of these triangles is meaningful.
1. Identify the Right Angles:
- Given that DA is perpendicular to AB and CB is perpendicular to AB, we can conclude that:
- Angle A (in triangle ABC) = 90°
- Angle B (in triangle DAB) = 90°
- Therefore, we have:
- Angle A = Angle B = 90°
2. Identify the Given Lengths:
- We are given that AC = BD.
- Therefore, we have:
- AC = BD
3. Identify the Common Side:
- The side AB is common to both triangles ABC and DAB.
- Therefore, we have:
- AB = AB (this is a common side)
4. Summarize the Pairs of Equal Parts:
- The three pairs of equal parts are:
1. Angle A = Angle B (both are 90°)
2. AC = BD (given)
3. AB = AB (common side)
5. Determine the Meaningfulness of the Statements:
- Now, we need to evaluate the two statements:
- (i) Triangle ABC is congruent to Triangle BAD.
- (ii) Triangle ABC is congruent to Triangle ABD.
- For statement (i), we can use the RHS (Right angle-Hypotenuse-Side) congruence rule:
- Both triangles have a right angle, the hypotenuses AC and BD are equal, and they share the side AB.
- Therefore, Triangle ABC ≅ Triangle DAB is a meaningful statement.
- For statement (ii), we cannot establish congruence because the angles and sides do not correspond correctly. Thus, Triangle ABC ≅ Triangle ABD is not meaningful.
Conclusion:
- The three pairs of equal parts are:
1. Angle A = Angle B
2. AC = BD
3. AB = AB
- The meaningful statement is (i) Triangle ABC ≅ Triangle DAB.
- Given that DA is perpendicular to AB and CB is perpendicular to AB, we can conclude that:
- Angle A (in triangle ABC) = 90°
- Angle B (in triangle DAB) = 90°
- Therefore, we have:
- Angle A = Angle B = 90°
- We are given that AC = BD.
- Therefore, we have:
- AC = BD
- The side AB is common to both triangles ABC and DAB.
- Therefore, we have:
- AB = AB (this is a common side)
- The three pairs of equal parts are:
1. Angle A = Angle B (both are 90°)
2. AC = BD (given)
3. AB = AB (common side)
- Now, we need to evaluate the two statements:
- (i) Triangle ABC is congruent to Triangle BAD.
- (ii) Triangle ABC is congruent to Triangle ABD.
- For statement (i), we can use the RHS (Right angle-Hypotenuse-Side) congruence rule:
- Both triangles have a right angle, the hypotenuses AC and BD are equal, and they share the side AB.
- Therefore, Triangle ABC ≅ Triangle DAB is a meaningful statement.
- For statement (ii), we cannot establish congruence because the angles and sides do not correspond correctly. Thus, Triangle ABC ≅ Triangle ABD is not meaningful.
- The three pairs of equal parts are:
1. Angle A = Angle B
2. AC = BD
3. AB = AB
- The meaningful statement is (i) Triangle ABC ≅ Triangle DAB.
Topper's Solved these Questions
Similar Questions
In a triangle ABC , if AB , BC and AC are the three sides of the triangle , then which of the following statements is necessarily true ?
View SolutionIn fig 7.13, AD=CDandAB=CB. (i) state the three pairs of equal in ΔABDandΔCBD. (iii) Is ΔABD[≡~?]ΔCBD ? Why or why not ? (iii) Does BD bisect ? ABC ? Given reasons
View Solution
Knowledge Check
If ΔABC~ΔDEF, then which of the following is true?
ABC.EF = AC.FDBAB.ED = AC.DECBC.DE = AB.EFDBC.DE = AB.FDIn isosceles triangle ABC, CA = CB = 4. which one of the following is the area of triangle ABC ?
A7B8C9DIt cannot be determined from the information givenIn triangle ABC, AB = 5 and AC = 3. which one of the following is the measure of the length of side BC?
ABC<7BBC=7CBC>7DIt cannot be determined from the information given
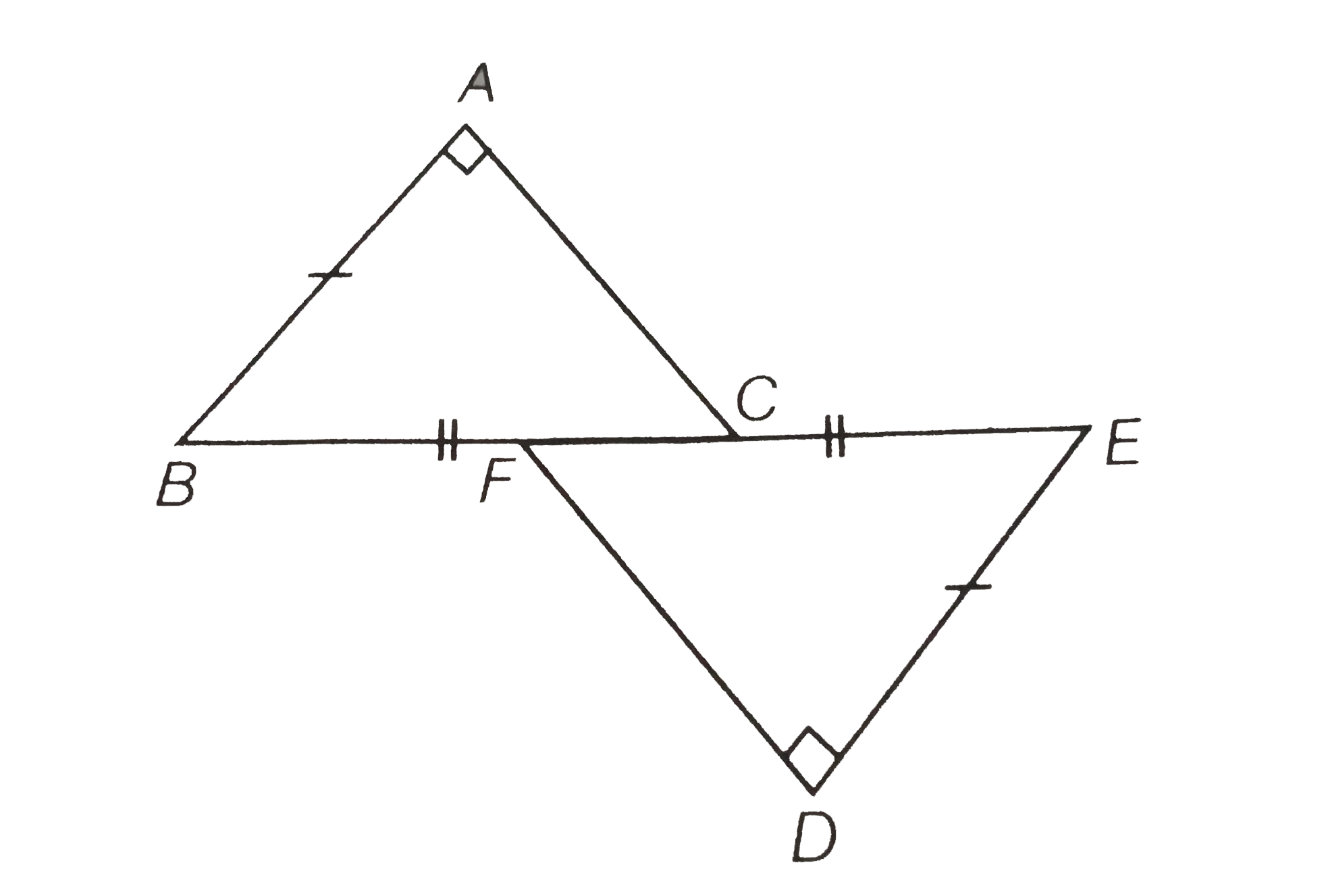
In figure ,BA⊥AC,DE⊥DF such that BA = DE and BF = EC. Show that ΔABC≅ΔDEF.
View SolutionIt is given that ΔABC≅ΔRPQ .Is it true to say that BC =QR ? Why ?
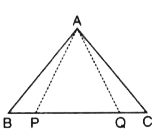
View SolutionThe given figure shows a ΔABC in which AB =AC and BP =CQ .
Prove that :
(i) ΔABQ≅ΔACP.
(ii) ΔAPQ is isosceles.
View SolutionIn ΔABC,if BC=AB and ∠B=80∘,then ∠A is equal to
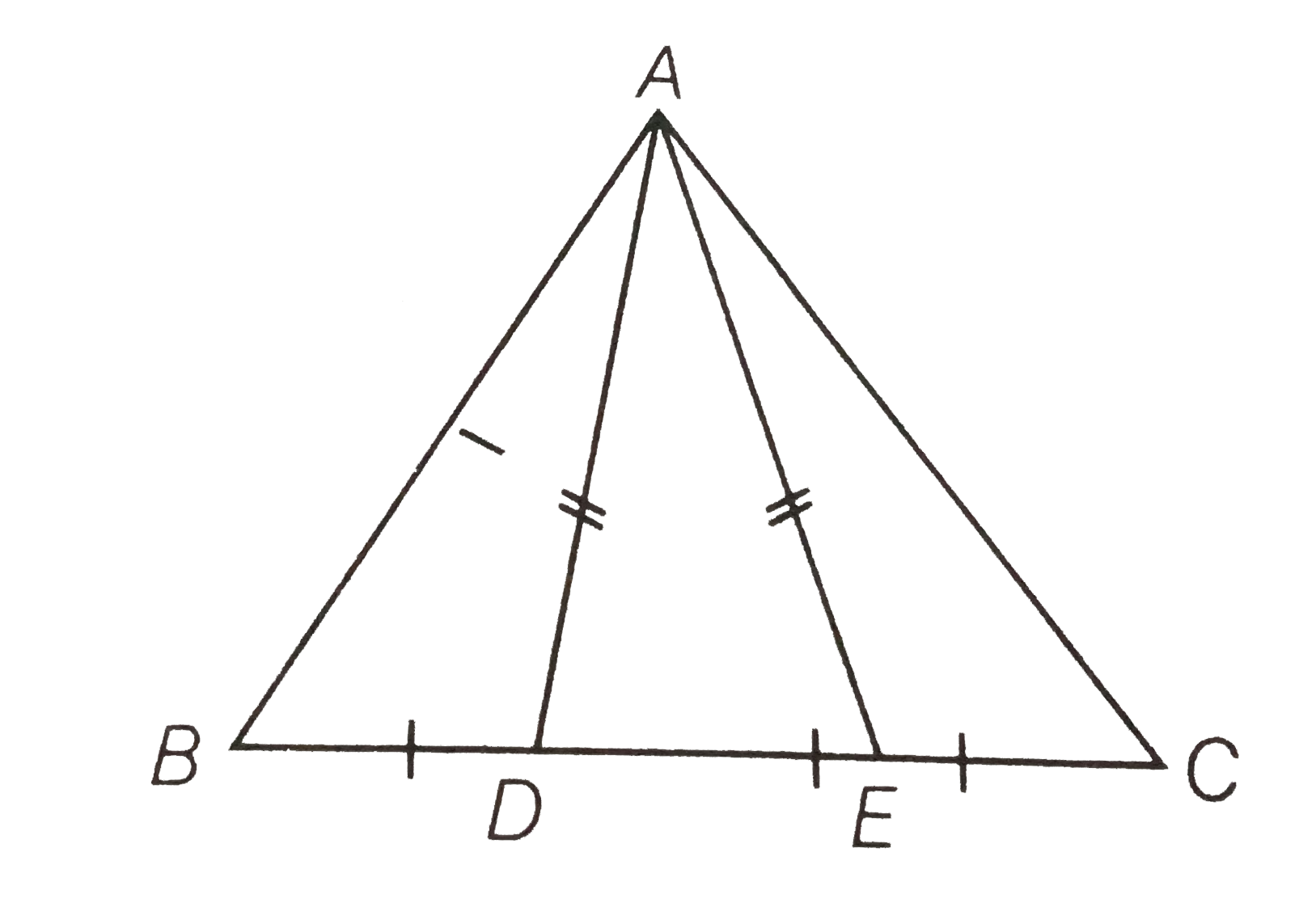
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
View Solution
